
Hinged Dissections: Swinging & Twisting
by Greg Frederickson, published by Cambridge University Press.
Hardcover: 2002, ISBN 0-521-81192-9. Paperback: 2010, ISBN-13 978-0-521-81192-7.

A geometric dissection is a cutting of a geometric figure into pieces that we can rearrange to form another figure. As visual demonstrations of relationships such as the Pythagorean theorem, dissections have had a surprisingly rich history, reaching back to Arabic-Islamic mathematicians a millennium ago and Greek mathematicians more than two millennia ago. As mathematical puzzles they enjoyed great popularity a century ago, in newspaper and magazine columns written by the American Sam Loyd and the Englishman Henry Ernest Dudeney. Loyd and Dudeney set as a goal the minimization of the number of pieces. Their puzzles charmed and challenged readers, especially when Dudeney introduced an intriguing variation in his 1907 book The Canterbury Puzzles. After presenting the remarkable 4-piece solution for the dissection of an equilateral triangle to a square, Dudeney wrote:I add an illustration showing the puzzle in a rather curious practical form, as it was made in polished mahogany with brass hinges for use by certain audiences. It will be seen that the four pieces form a sort of chain, and that when they are closed up in one direction they form a triangle, and when closed in the other direction they form a square.This hinged model, has captivated readers ever since. There is something irresistible about the idea of swinging hinged pieces one way to form one figure, and another way to form another figure. You do not really need a physical model to enjoy this property. Once you have examined this figure, you will be swinging mental images of the pieces around in your mind.
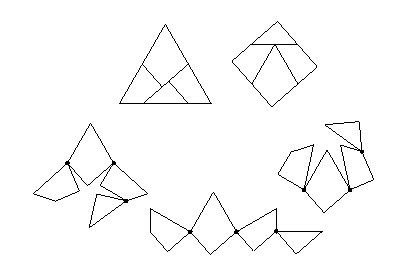
When I wrote my first book on geometric dissections, I became fascinated with hingeable dissections. I explicitly illustrated hingings in 18 figures and identified the hingeability of a number of others. I discovered that many hingeable dissections have been published without any indication that they are hingeable. There were enough that I wondered about the following question: Given any pair of figures that are of equal area and bounded by straight line segments, is it possible to find a hingeable dissection of them?
I haven't found an answer to this question, but as I worked on it, I found lots and lots of nifty hinged dissections. Most of them are two-dimensional, although I do have a chapter on three-dimensional hinged dissections. For three-dimensional dissections, I first considered the "piano hinge", which is the obvious analog of the "swing hinge" above. But I also thought about alternative types of hinges, which led me in turn to a basic hinge for two-dimensional dissections that no one in the field of dissections had thought about. I call this new hinge a "twist hinge". I have discovered a surprising wealth of twist-hinged dissections, which I explore in the last two chapters of my book. You can ask the same question about twist-hinged dissections as I have about swing-hinged dissections. And I don't know the answer to that question either.
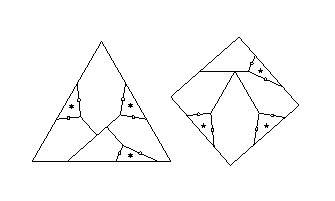
Below is a twist-hinged dissection of an equilateral triangle to a square. A small circle on an edge indicates the position of a twist hinge. A piece that is labeled with an asterisk in the equilateral triangle is flipped over an odd number of times in converting to the square.
Considering the pivotal role that Henry Dudeney and his hinged model play in this second book of mine, I was a bit daring in my multi-segment "Curious Case" feature. I hope that I didn't truly anger any Dudeney enthusiasts. I just called it as I saw it. And I hope that readers will understand that I harbor a real reverence for Henry Dudeney. To prove it, I refer you to a song that I wrote for him in 2017: "A Puzzlist (Mathematical)
Check out my third and fourth books too! :
Piano-hinged Dissections: Time to Fold! - a book about dissections that fold.
Ernest Freese's Geometric Transformations: the Man, the Manuscript, the Magnificent Dissections! - the title says it all.
Recent excitement (for me, anyway!):
GeoGebra Animations of Hinged TessellationsAlfinio Flores published an article "Hinged Tilings" in volume 6, number 1 of the North American GeoGebra Journal that describes hinged tessellations, which I had discussed in my "Turnabout 3: Hinged Tessellations". Click on the above link to view the article.
The article provides links to various animations (in GeoGebra) of many examples that I had shown. To play with the animations, click this next link and then click on any figure to select an example. Then click and drag on the indicated hinge in an example, and you will then being flexing the hinged tessellation. Enjoy!
(Note that you should not drag the indicated hinge too far, because the GeoGebra code does not prevent weirdness such as you pulling pieces through each other!)
My Keynote Lecture at Shape Modeling International 2012 - May 2012I was invited to give a keynote lecture at Shape Modeling International 2012, held at Texas A&M University, in College Station, Texas, May 22-25. Not all links in the above are still active, but if you click on my link "Beyond Swinging: Hinged Dissections that Twist or Fold" you will at least get a short summary of my talk, and also a short biography of me. See the CS department news item: (link no longer active) Frederickson Keynote Speaker at 2012 Shape Modeling International Conference.
My Parade of Algorithmic Mathematical Art! - August 2011In May and June of 2011, I collected together the set of animations and videos that I had created for my various talks during the period 2007-2011. With the help of Charlie Fultz, I produced a 20-minute-long presentation that is part of a 3-artist exhibition in the Lawson Computer Science Building for the academic year 2011-2012. My work will be on display in a cabinet adjacent to the elevator on the second floor of the building. In addition to my artist's statement, the cabinet will contain a Sony S-Frame that will continuously run my presentation, laser-cut wooden models of three of my folding dissections, and copies of my three books on geometric dissections. Announced on September 12, 2011 in Purdue Today, my work is part of a three-artist exhibition (with Petronio Bendito and David Spellmeyer) Art Comes to Lawson, installed for the fifth-year celebration of the Richard & Patricia Lawson Computer Science Building. Read the interview with me and Petronio in Purdue Today.
Animations of dissections with special properties! - November 2010I have posted a webpage containing animations of hinged dissections of various types.
These hinged dissections are discussed in my article, "Hugo Hadwiger's influence on geometric dissections with special properties," which was invited to a special edition of Elemente der Mathematik celebrating the centennial of the Swiss Mathematical Society.
Dimensions of Discovery! - September 2009The cover of the inaugural issue of Purdue University's Dimensions of Discovery sports a montage of journal and book covers that includes the one with a picture of the swinging tables discussed in my article, "Designing a Table both Swinging and Stable", College Mathematics Journal, vol. 39, no. 4 (September 2008), pp. 258-266. Can you spot my cover amongst the 60-some odd covers?
Animations of square dissections! - September 2009I have posted a webpage containing animations of swing-hinged dissections of squares.
These swinging squares are discussed in my article, "Polishing some Visual Gems," Math Horizons, September 2009, pp. 21-25.
Dirk Huylebrouck's architecture students build my twist-hinged benches - May 2009I have created a webpage that links to two YouTube videos that demonstrate models of my twist-hinged dissection of ring benches,
which I presented at the Bridges Donostia conference in San Sebastian Spain in July 2007. The models were built, and the video was shot, by Dirk Huylebrouck's architecture students at Sint Lucas (Brussels, Belgium). They're great!
Hinged dissections are once again the rage in France! - January 2009There has been major new excitement with respect to hinged dissections since Timothy G. Abbott, Zachary Abel, David Charlton, Erik D. Demaine, Martin L. Demaine, and Scott D. Kominers published their paper, "Hinged Dissections Exist," in June of 2008. (See "Open question resolved!".) Now this excitement has crossed the Atlantic Ocean: Jean-Paul Delahaye has written another article on hinged dissections, "La géométrie du bricolage" ("The geometry of amateurs"), for his column entitled "Logique et calcul" ("Logic and calculation"), for Pour La Science, the French edition of Scientific American. The article appears in Number 374 (December 2008) on pages 100-105.
Animations of swing-hinged table tops! - June 2008I have posted a webpage containing animations of swing-hinged dissections of triangular to square table tops.Animations of twist-hinged ring benches! - August 2007
These swinging tables are discussed in my article, "Designing a Table both Swinging and Stable", College Mathematics Journal, vol. 39, no. 4 (September 2008), pp. 258-266.I have posted a webpage containing a number of twist-hinged dissections of ring benches.
I demonstrated these animations at the Bridges Donostia conference in San Sebastian Spain in July 2007. The corresponding paper is in the proceedings on pages 21-28.
Here is an updated version reflecting additional material to the talk after I sent in the proceedings version of the paper.
And here is a revised version of that later version, which I have now submitted to a journal.
Twist-hinged animations! - June 2007I have posted a webpage containing a number of wild twist-hinged dissections.
I first demonstrated these animations at the 7th Gathering for Gardner in 2006, and they are meant to be a supplement to an article that is to appear in the Mathematical Intelligencer.
A hinged dissection in a lesson plan! - January 2006Pat Baggett and Andrzej Ehrenfeucht posted a lesson plan based on the swing-hinged dissection of the equilateral triangle to the square: Triangle to square: A hinged dissection.
I especially like the way the hinges are incorporated into the design, using the thick foam rubber that makes up the pieces. Nifty! And the animations on the webpage are really effective, too.
Animations in wood and java! - October 2005After seeing David Gunderson's wooden models of
Students swing! - June 2003Middle school math teacher Kim Sharp got his pre-algebra class swinging in the classroom aisles!
He called it `Springtime Swingtime'!
Great review in American Scientist! - May 2003Mike Eisenberg wrote an enthusiastic review for the May-June, 2003, issue of American Scientist. The review, entitled "King of Swing," concludes with:"I would put Frederickson's dissection books, along with Alan Holden's Shapes, Space, and Symmetry (Columbia University Press, 1971), on the shortlist of beautiful, inspirational and accessible works in recreational geometry. I heartily recommend Hinged Dissections to anyone who loves geometry, or wants to."
Hinged dissections classified as Art! - April 2003Joe Malkevitch, a professor of mathematics at York College (CUNY-The City University of New York), wrote a monthly essay, "What's New in Mathematics" for the American Mathematical Society. His column for April, 2003, was "Mathematics and Art." See Section 5, "Polyhedra, tilings, and dissections," which referred to some of my work, in particular, photos of models of my hinged dissections.
Chemists discovered (hinged) dissections! - January 2003The chemists do their version of `Look, Ma - No hands'
Hinged dissections established a beachhead in France! - December 2002Jean-Paul Delahaye wrote a column entitled "Logique et calcul" ("Logic and calculation"), for Pour La Science, the French edition of Scientific American. In the December 2002 issue (number 302) of Pour La Science, he wrote about the book and related material in "Découpages articulés" ("Hinged dissection"), pages 164-169.
AMS took notice of hinged dissections! - December 2002The Notices of the AMS (American Mathematical Society) listed the book in its Book List on page 1408 of Volume 49, Number 11 (December 2002). As explained at the beginning of the section:"The Book List highlights books that have mathematical themes and hold appeal for a wide audience, including mathematicians, students, and a significant portion of the general public."The listing continued in succeeding issues, but was gone in December 2003.
More information:
Table of contents.
Comments, reviews, and news.
Updates and corrections.
Exact measurements for the swing-hinged triangle to square dissection.
A photo gallery.
A video gallery.
Past and future events.
Education.
Citations.
Have you seen my article in the summer 2001 issue of the Mathematical Intelligencer?
On the table of contents page, there is a picture of me manipulating a model of my twist-hinged dissection of an equilateral triangle to a square.
Related to this dissection, there is a (minor) mistake in one of the figures. Here is a correction.
Last updated October 4, 2018.