
Piano-hinged Dissections: Time to Fold!
by Greg Frederickson, A K Peters Ltd, 2006, ISBN 156881299X (hardcover).
(Since 2012, handled by Taylor & Francis Group, LLC)

A geometric dissection is a cutting of a geometric figure into pieces that can be rearranged to form another figure. For two-dimensional figures, they are striking demonstrations of the equivalence of area, reaching back to the classical Greek era and to the zenith of Arabic-Islamic culture. Dissections became increasingly popular during the last century, after the mathematical puzzlists Sam Loyd and Henry Ernest Dudeney first included them in their newspaper and magazine columns. (See my original book for more information on the general subject of geometric dissections.)
Some dissections have a nifty property that results from hinging the pieces together in a certain way. We can then form one figure by sweeping the pieces one way on the hinges, and the other figure when we sweep them the other way. Almost a century ago, Dudeney introduced perhaps the best-known such dissection, of an equilateral triangle to a square. Under the spell of such hinged dissections, I wrote a surprising book on the subject. That book explores not only dissections in which we "swing" the pieces around, but also dissections in which we "twist" the pieces around.
Now it's time for a different kind of hinge - a piano hinge - which allows two flat pieces to fold together or apart. (The term piano hinge comes from the long hinge that attaches the lid of a grand piano to the box containing the strings.) We can treat each polygon as a shallow prism separated into two levels which we would dissect further into flat pieces. A piano-hinge can bring two flat pieces that are side-by-side on the same level to be one on top of the other. This hinging motion is essentially what you get when you fold a piece of paper. Thus those of you who enjoy origami, the Japanese art of paper folding, may also enjoy piano-hinged dissections.
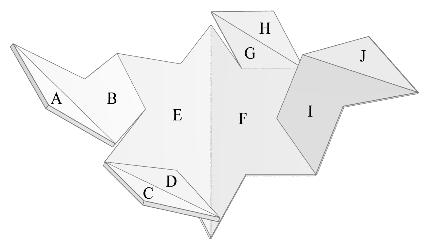
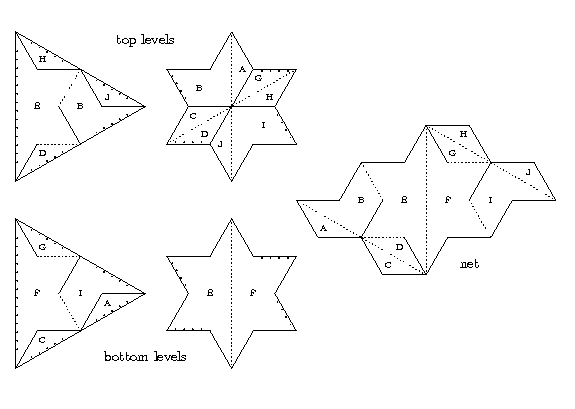
A beautiful example is of a 10-piece dissection of a hexagram to an equilateral triangle, with the unfolded "assemblage" shown above in perspective. Below, I use a diagram to further describe the dissection. I indicate a piano hinge that connects a piece on the top level to a piece on the bottom level by a line of dots next to the hinge line on each of the two levels. I indicate a piano hinge between two pieces on the same level, by a true dotted line segment. In the figure below, piece E on the top level of the triangle hinges with piece F on the bottom level. In the hexagram, E and F still share a hinge, but both now sit side by side on the bottom level. In this dissection, all of the pieces can fold out flat into the net shown on the right, below.
At first it was really difficult figuring out how to design piano-hinged dissections. Getting the pieces to land in the right place after several cuts and folds was decidedly tricky. Even after the first dozen or so successes, I wasn't sure that I could identify enough interesting material to fill this book. The progress in terms of the number of dissections was slow, sometimes frustratingly so. Yet, one insight at a time, I built up my stockpile of useful techniques, exciting dissections, and intriguing properties. As I gained confidence, I was amazed by the mind-boggling transformations made possible by the simple operation of folding.
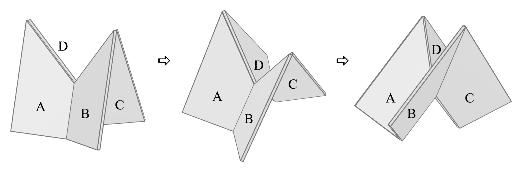
I was stunned by the beauty of many of the dissections. And the best of the bunch still produce a sense of wonder in me. How could I resist the elegant hinging of the mitre to the gnomon below? (Note: To get the mitre, take the figure on the left and flatten pieces A and B completely on top of pieces D and C. To get the gnomon, take the figure on the right and flatten pieces B and C completely on top of pieces A and D.) This dissection is a example of cycle of four pieces, each of which is hinged to its predecessor and successor in the cycle. (The cycle is piece A, piece B, piece C, piece D, and then back around to piece A again.) What's especially remarkable is that the four angles that meet at the center of the cyclic hinging sum to more than 360 degrees. One consequence of this fact is that when we fold from the mitre to the gnomon, the surfaces that were on the outside go to the inside, and vice versa. Neat!
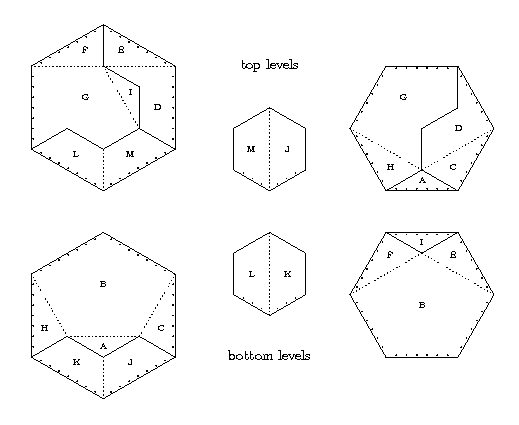
We can also have cyclic hingings in which the four angles that meet at the center of the cyclic hinging sum to less than 360 degrees. There are three such cyclic hingings in the dissection of hexagons in the figure below. Each of them looks like a "cap" when they are folded halfway between one flat figure and the other flat figure. And look how the cyclic hingings are placed: At three vertices (every second one) in the largest hexagon, at two vertices (every third one) in the middle hexagon, and at a single vertex in the smallest hexagon. Again, how neat!
To help readers visualize the piano-hinged dissections, I've included line drawings of all of the dissections, as well as perspective views of most of the dissections. Yet even those perspective views aren't always enough to convey the excitement. So, I've produced a CD containing video clips to bring a number of the dissections to life. Just pop the CD into a laptop computer, and enjoy an hour of folding and flapping. (On a Windows machine, you view it using Media Player. On an Apple machine, you can view it using Quicktime, if you download free software from Microsoft that adapts Quicktime to read wmv format.) With many of the models in bright colors, and the rest of the models out of lovely wood, it's great viewing!
As you explore this enchanting new topic with the help of the figures and videos, you may well conclude that piano-hinged dissections are challenging to discover and difficult to illustrate. Yet paradoxically, you need relatively little background to understand and enjoy them. As with my earlier books, the intended audience is anyone who has had a course in high school geometry and thought that regular hexagons were rather pretty. You should find it easy to make passable models of many of the piano-hinged dissections, if you cut them out of, for example, a manila folder and use a normal adhesive tape.
In addition to presenting the piano-hinged dissections, I couldn't resist sharing the latest news about (general) geometric dissections: I was lucky to have played a key role in locating what had been a "lost" manuscript on geometric dissections. The author of the manuscript, Ernest Irving Freese, was an architect in Los Angeles who, near the end of his life, became passionate about dissections. Besides cataloging known dissections, he invented many new ones, some rather brilliant, and a few which have served as the basis for some of my piano-hinged dissections. I'm pleased to give you a sneak preview of his work in a five-part series sprinkled throughout my book.
You may also enjoy the short sections that I have written on related folding topics. Charmed by the standard calculus problem of cutting and folding a rectangular sheet to form a box of maximum volume, I wrote an article on both its history and a new, improved solution that I discovered. The article, now included in this book, won the Polya Award for expository writing from the Mathematical Association of America. I have also crafted two additional short sections, one on folding blocks of stamps and the other on folding maps and square twists.
All in all, creating this book has been a remarkable experience for me. I certainly hope that you will have fun with it too.
Recent excitement (for me, anyway!):
My paper, "Folding hexagons, dodecagons, and dodecagrams," -- July 2013
at Bridges Enschede 2013: Mathematics, Music, Art, Architecture, Culture},
in Enschede, the Netherlands. (Okay, Dutchophiles: How is that pronounced?)See my webpage containing animations and videos of folding dissections for this paper.
Article on polyominoes that fold from one level to two - September 2011In 2009 I explored techniques for folding a polyomino that is one level thick to the same figure that is two levels thick.
This resulted in an article,"Folding Polyominoes from One Level to Two", by Greg N. Frederickson,I have posted a webpage containing a variety of such polyomino folding dissections.
College Mathematics Journal, vol. 42, no. 4 (September 2011), pp. 265-274.
At the annual meeting of the Pacific Northwest Section of the MAA, at the University of Portland, in Portland, Oregon, on April 20-21, 2012, the undergraduate student Jakob Daum, at George Fox University, presented a poster with the same title as my article, and presumably presenting material covered by my article. I am pleased that my article has served as a stimulus to an undergraduate.
Video of piano-hinged pentominoes to squares - January 2010Daniel Wyllie Rodrigues has posted on YouTube some lovely video of piano-hinged dissections of various pentominoes to squares. Bravo!
More animations of folding figures - May 2009I have posted a webpage containing more folding dissections. I demonstrated these animations at the DIMACS Workshop on Algorithmic Mathematical Art: Special Cases and Their Applications, May 11-13, 2009.
Animations of folding figures - April 2008I have posted a webpage containing a number of folding dissections. I demonstrated these animations at the Gathering for Gardner in Atlanta in March 2008. Also, the corresponding paper is posted.
More information:
Table of contents.
Publisher's webpage for the book.
Adjusting the display for the videos.
Comments, reviews, and news.
Updates and corrections.
A photo gallery.
Past and future events.
Citations.
Education.
Last updated June 13, 2014.