
Dissections: Plane & Fancy
by Greg Frederickson, published by Cambridge University Press.
Hardcover: November 1997, ISBN 0-521-57197-9. Softcover: February 2003, ISBN 0-521-52582-9.

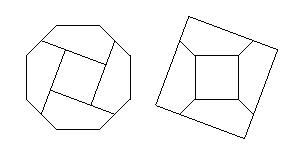
My book explores an area of mathematical recreations, called geometric dissections. A geometric dissection is a cutting of one or more figures into pieces that can be rearranged to form other figures. With an emphasis on using as few pieces as possible, these geometrical puzzles have prompted ingenious approaches, leading to many beautiful and elegant constructions. An example is the remarkable 5-piece dissection of a regular octagon to a square.
I have included not only earlier dissections but also much new unpublished material by myself and others. The discussion highlights the techniques and their underlying mathematical properties, and is accompanied by hundreds of diagrams. Special attention is paid to historical origins, transporting the reader to the palace school of the tenth-century Baghdad caliphate, to the mathematical puzzle columns in turn-of-the-century newspapers, and to the 1900 Paris Congress of Mathematicians. Short biographies flesh out the lives of the people - famous, not-so-famous, and obscure - who have worked on these problems. Marvelous illustrations are reproduced from the book Cyclopedia of Puzzles by Sam Loyd.
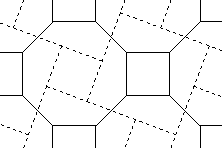
Returning to the example of a regular octagon to a square: The dissection can be generated by the "completing the tessellation" technique (which I explain carefully, along with many other solution methods). The books on mathematical recreations attribute the octagon-to-square dissection to James Travers, but they are all wrong. It appeared earlier, in a puzzle column by Henry Dudeney, where it was attributed to a Dr. G. T. Bennett. And just who was G. T. Bennett?: Check out his biography in the book!
But wait! From information not available to me when I published this book, I have learned that this dissection was known approximately 700 years ago. For the inside scoop, see my new book, Hinged Dissections: Swinging & Twisting, Cambridge University Press, 2002.
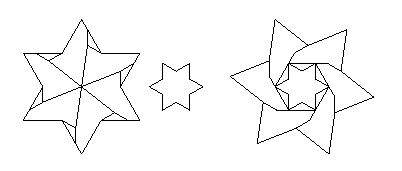
To give a hint of the wealth of new dissections in the book, my dissection of two hexagrams (6-pointed stars) to one is illustrated above. The method works not just for the particular dimensions shown, but for any in which the ratio of the sidelength of the medium-sized star to that of the small star is at least the square root of 3. The dissection is a great example of rotational symmetry, in this case 6-fold symmetry. I named this dissection "Star Genesis". Do you see why?
And here is a puzzle that is original: Cut a square of sidelength 17 into only four pieces that reform to make two squares, of sidelengths 8 and 15. Puzzlists had known how to find 4-piece dissections for squares of sizes 3, 4, and 5, for 5, 12, and 13, for 7, 24, and 25, and so on. But the solution methods for those cases do not seem to work for 8, 15 and 17. You can find the 4-piece solution to this puzzle in my book. Or, if you need some help, here is a hint.
Don't miss my second, third, and fourth books! :
Hinged Dissections: Swinging & Twisting. A book exclusively about hingeable dissections!Piano-hinged Dissections: Time to Fold!. A book about a new type of dissections — folding dissections!Ernest Irving Freese's Geometric Tranformations: the Man, the Manuscript, the Magnificent Dissections!. The book's title says it all!
Article on Cube Dissections
Catch my article on an infinite family of cube dissections: "Casting light on cube dissections".
I've created some nifty animations to accompany the article on dissections!
Gavin Theobald's dissections
Over the last several years, Gavin Theobald has created a wonderful website, Geometric Dissections. It includes not only many of the dissections that he had found prior to 1997, but an increasing number of remarkable dissections that he has found since then. Of particular note are his dissections of regular polygons to squares---feast your eyes on the dissection of the {11}, or the {17}, or the the {21}, ... He also has dissections of all stars up to 10 points, plus the 12-pointed stars too.
Gavin has also extensively studied strip methods, identifying a number of amazing variations of the P and T methods first enumerated by Harry Lindgren. He includes some intriguing examples in his discussion.
Geometric dissections and occupational therapy!
A standardised cognitive test for testing memory in brain-injured people has recently been revised to include, among other new features, a geometric dissection! The dissection facilitates measuring how well the patient can learn a new skill.
New - the chemists discover (hinged) dissections!
The chemists do their version of `Look, Ma - No hands'
New - a nifty puzzle by Bernard Lemaire!
Dissect a cross to a square.
Two cartoons by Dale Taylor!
from NotInMyBackyard! (approx 57K). Dissections in the doghouse!
Fresh from the silk screen:
Plane & Fancy T-shirts (approx 100K). Fashion statements that celebrate dissections!
Hole Dissections: Something Old and Something New!
My Hole Dissections
More information about the book:
Table of contents.
Comments, reviews, and news.
References on the web.
Updates and corrections.
More dissection news.
A photo gallery.
A video gallery.
Past and future events.
Education.
Citations.
More fun stuff with dissections:
Animation of hinged dissections by Alain Rousseau
Geometric dissections on the web.
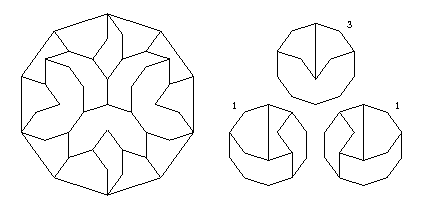
A dissection of five regular decagons to one:
A special thanks to Martin Gardner who is in more ways than one the godfather of this book.
An excerpt from Winfried Scharlau's novel (in German), Scharife, which he describes the hold that dissections can have over someone.
Last updated December 10, 2019.