2.2 Nonlinear Solutions of f(x)=0

[1.2 Binary Numbers] [1.3 Errors] [2.1 Interation x=g(x)] [2.2 Nonlinear Solutions of f(x)=0]

Bisection Method

- Similar to binary search

Starting with two numbers a and b such that
1. a<b
2. ( f(a)<0 and f(b)>0 ) or ( f(a)>0 and f(b)<0 ) ie f(a) and f(b) have different signs and neither are 0

This means that there is an x in [a,b] such that f(x)=0

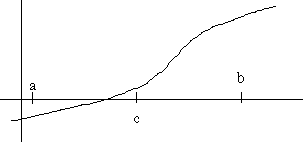
c is the average of a and b ( c = (a + b)/2 )

If f(a) and f(c) have opposite signs, then a zero lies in [a,c]
Otherwise a zero lies in [c,b] but if f(c)=0 then c is a zero so stop

Example:

sin(x)=1/2 (x in degrees)
f(x) = sin(x) - 1/2 = 0
start for example, with a=0 and b=50 f(0)= sin(0) - 0.5 = 0 - 0.5 = -0.5
f(50)=sin(50) - 0.5 = 0.266

f(a)<0 and f(b)>0 ==> OK

a	b	c	f(c)
0	50	25	-0.077
25	50	37.5	0.1087
25	37.25	31.25	0.018
25	31.25	28.125	-0.02

c approaches 30

Error

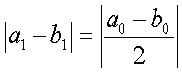
At step n,

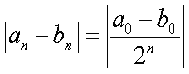
If we want to approximate with error < E how many steps do we need?

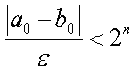
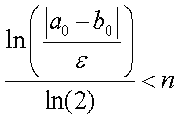
Example:

From previous example, if we need to approximate with E < 0.01:

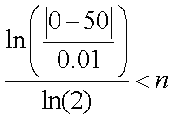
which yields

So we pick n to be 13 (ie we will iterate 13 timesto be sure we have an error less than 0.01)

False Position (Regula Falsi)

	Similar to bisection method
	Requires an interval [a,b] where a zero is found
	converges faster than bisection

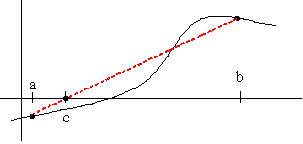
A line is subtended between (a,f(a)) and (b,f(b))
(c,0) is the intersection of the line and the x-axis
If f(a) and f(c) have opposite signs, then a zero lies in [a,c]
Otherwise a zero lies in [c,b] but if f(c)=0 then c is a zero so stop

How to compute c?

We know:

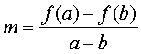
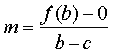
so combine those two:

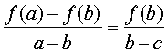
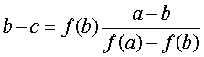
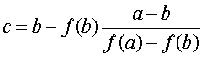
Example:

sin(x) = 1/2 f(x) = sin(x) - 1/2 = 0
Start with a=0, b=50

Iteration	a	f(a)	b	f(b)	c	f(c)
0	0	sin(0) - 0.5= -0.5	50	1.266	32.637	sin(32.637) = 0.0393
1	0	-0.5	32.637	0.0393	30.259	0.0039
2	0	-0.5	30.259	0.0039	30.0248	0.000375

When to stop the iterations?

When the method converges to the desired percision

Horizontal Convergence
Instead of expecting f(x)=0, expect f(x) to be within a small error E:

Example: If E=0.001 in the previous example then we would stop at iteration 2

Geometrically, this means that the zero is in a horizontal band

Vertical Convergence
Stop when x is at a distance <delta> away from P (the solution)

	However, it is impossible to find <delta> since that implies we know P (the exact solution)
	Since we know the error gets smaller at every iteration we can determine that
	Geometrically this means:

Horizontal & Vertical Convergence
Use both horizontal and vertical convergence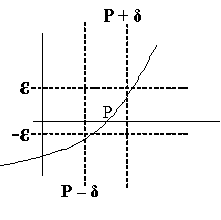

AND

Troublesome finctions

If the graph y=f(x) is steep near the root (P, 0) then the root finding is well conditioned

A solution with good precision is easy to obtain

If the graph y=f(x) is shallow near (P, 0) then the root finding may only have a few significant digits.

Webpage by Emil Stefanov