[ Index ]

[1.2 Binary Numbers] [1.3 Errors] [2.1 Interation x=g(x)] [2.2 Nonlinear Solutions of f(x)=0]

2.1 Interation x=g(x)

Solution of nonlinear equations of form f(x)=0

- We will use iteration to solve these equations

Starting with a value of P0 and a function Pk+1=g(Pk) evaluate P1, P2, P3
P0
P1=g(P0)
P2=g(P1)
...
Stopping criteria: | Pk - Pk+1 | < E

Fixed Point - A fixed point of g(x) is a real number p such that p=g(p)

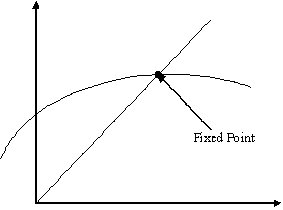Geometrically, the fixed points of a function y=g(x) are the points of intersection of y=g(x) and y=x

Fixed Point Iteration - An equation of the form Pn+1 = g(Pn) for n = 0, 1, 2, ...

Example:
x2 - 2x + 1 = 0s

Get a fixed point iteration equation
x2 - 2x + 1 = 0
x=(x2+1)/2
xk+1 = (xk2+1)/2

Assume x0 = 0,
x1 = (02+1)/2 = 0.5
x2 = (0.52+1)/2 = 0.625
x3 = 0.695
x4 = 0.74
x5 = 0.77
x6 = 0.79
x7 = 0.82
x8 = 0.83
...
xinf = 1

Fixed Point Theorem

bulletIf

for all x in [a,b] and all g(x) in [a,b]
then the iteration Pn = g(Pn-1) will converge to a fixed point p in [a,b]. In this case, O is said to be an attractive fixed point.
bulletIf

then the iteration Pn = g(Pn-1) will diverge.

Two cases for convergence and divergence

bulletMonotone Convergence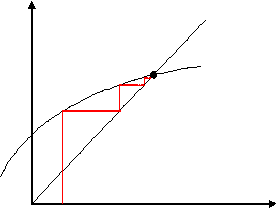

bulletThe acute angle between the tangents of g(x) and the x-axis theta must be:
bulletOscillating Convergence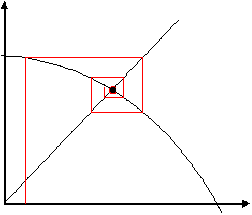


bulletThe acute angle between the tangents of g(x) and the x-axis theta must be:
bulletMonotone Divergence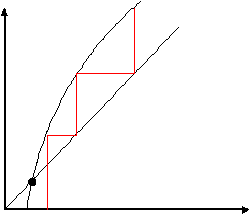

bulletOscillating Divergence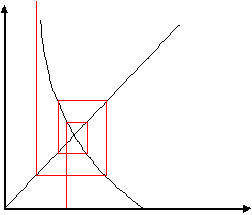


 

Example: Divergence

In the previous example g(x) = xk+1 = (xk2+1)/2
g'(x) = (1/2)(2x) = x
therefore the iteration will only converge if x0 was between -1 and 1

As long as | g'(x) | < 1 and y = g(x)
x is in [a,b]
y is in [a,b]
then it will converge

Let x0 = 2 in the previous example
x1 = (22+1)/2 = 2.5
x2 = 3.625
x3 = 7.07
x4 = 25.495
...
xinf diverges

Webpage by Emil Stefanov