1.3 Errors

[1.2 Binary Numbers] [1.3 Errors] [2.1 Interation x=g(x)] [2.2 Nonlinear Solutions of f(x)=0]

1.3 Errors

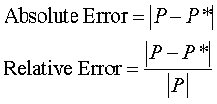
Chop-off vs. Round-off

Example:
Pi=3.141592654...
use 3 digits for fraction:
Chop-off: 3.141
Round-off: 3.142
Round-off is more accurate since it produces the least relative error

Propagation Errors

Assume p and q are approximated by p* and q* such that:
p*=p+ep, q*=q+eq

Sum: p* + q* = p + q + (ep + eq)

(ep + eq) is the new error

The new error is the sum of the errors

Product: p* q* = (p+ep)(q+eq)=pq+p(eq)+q(ep)+(ep)q+(ep)(eq)

The new error depends on p and q

The new error is amplified by the magnitude of p and q

Algorithm stability

An algorithm is:

	Stable - If small initial errors stay small
	Unstable - If small initial errors get large after several iterations

Webpage by Emil Stefanov