[ Index ]

[1.2 Binary Numbers] [1.3 Errors] [2.1 Interation x=g(x)] [2.2 Nonlinear Solutions of f(x)=0]

1.2 Binary Numbers

Q:    Why do we use binary numbers?
A:    We use binary numbers because it was easy to implement with circuits. Binary only requires two states: "ON" and "OFF"

Example:    537.510 = 1 x 29 + 0 x 28 + 0 x 27 + 0 x 26 + 0 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 + 1 x 2-1

How to get from base 10 to base 2
Separate the integer part from the fraction part: N.F
The integer part can be represented as


We wish to find the digit bi (0 or 1)
We divide by 2:

The remainder determines if b0 is 0
- Repeat until the integer part is 0

Example: How to convert 34 in base 10 to binary (base 2)
34/2 = 17 R 0 ==> 0
17/2 = 8 R 1 ==> 1
8/2 = 4 R 0 ==> 0
4/2 = 2 R 0 ==> 0
2/2 = 1 R 0 ==> 0
1/2 = 0 R 1 ==> 1

So 3410 = 1000102
Note : The binary representation is the reverse of the 1's and 0's obtained by dividing

Example:
0.12 = 1*2-1 = 1/2
0.012 = 1*2-2 = 1/4
0.112 = 1*2-1 + 1*2-2 = 1/2 + 1/4 = 3/4

Q:    What about 1/3?
A:    1/3 = .3333 = 1/2 * 0 + 1/4 * 1 + 1/8 * 0 + 1/16 * 1 + ... = 0.01010110

Representation of numbers in the machine

Two common representations:
1. Fixed Point
2. Floating Point

Fixed Point
The number of bits for the integer part and the fraction part are fixed

Example: NNNN.FF2 has 4 bits for the integer part and 2 bits for the fraction
This  is just an example: usually you would give more bits for for both the integer part and the fraction.
For example: 2 bytes for the integer and 2 bytes for the fraction

Advantages of fixed point:

bulletFast arithmetic - Uses integer arithmetic
Example:
       1.0 1     =   1.25
+  1 0.1 0    =    2.5
--------------------------
    1 1.1 1    =    3.75
bulletUsed in in signal processors and signal processing programs that require real time operations
Example: MP3 Player, MP3 Encoder/Decoder, MPEG, etc

Disadvantages of fixed point:

bulletVery restrictive range
bulletBad precision
bulletSmallest number is restricted to the number of bits used in the fraction
bulletGenerates a lot intermediate of errors during operations

Floating Point
The decimal point moves around to keep the desired precision.
Uses scientific notation:

Q is called the mantissa
N is called the exponent

The precision of the number depends on the number of bits used to represent Q.
The numbers are represented in the computer as

where Q and N are represented by a fixed number of bits.

Uniqueness

To have a unique representation for each number, numbers are normalized or adjusted so that

except for 0. The uniqueness is useful for some operations such as checking for equality.

Example:    Adding (1/3 + 3/5) + 1/15

Assume 4-bit mantissa and 2-bit exponent

1/3 = (.010101...)2 * 20 = (.10101...)2 *2-1 =>(.1011)2 *2-1
3/5 = (.1000110011...)2 * 20 => (.1010)2 * 20

Adding 1/3+3/5

Normalize the largest exponent before addition
Note: Result has the larger of the two exponents


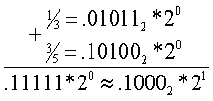
Note: When processors add numbers, they use registers twice as big for the computation.

Adding 1/15 to the previous result

1/15 = (.100010001...)2 * 20 => (.1001)2 * 2-3

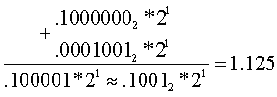
Since 1/3 + 3/5 + 1/15 = 1 and our result was 1.125, then there was an error due to the very small mantissa.

Modern architectures give 2 options to represent real numbers:

bulletSingle precision (float)
bulletuses 4 bytes (32 bits)
bullet24 bit mantissa (1 bit for sign)
bullet8 bit exponent (1 bit for sign)
bulletRange is 2-128 to 2127
bulletAccuracy is the smallest difference between 2 numbers with exponent
Example: 10000 is 2-23 and you have about 6 decimal digits of precision.

 

bulletDouble precision (double)
bulletuses 8 bytes (64 bits)
bullet53 bit mantissa (1 bit for sign)
bullet11 bit exponent (1 bit for sign)
bulletRange is 2-1024 to 21023
bulletAccuracy is 2-52 => 2.2*10-16 (about 15 digits of accuracy)

Webpage by Emil Stefanov