

Next: Mathematical Software
Up: VITA WALTER GAUTSCHI
Previous: Translations
1951
- Ein Analogon zu Grammels Methode der graphischen Integration
gewöhnlicher Differentialgleichungen, Z. Angew. Math. Mech. 31,
242-243.
1953
- Fehlerabschätzungen für die graphischen Integrationsverfahren
von Grammel und
Meissner-Ludwig, Verh. Naturforsch. Ges. Basel 64,
401-435.
1954
- Über die zeichnerischen Ungenauigkeiten und die zweckmässige
Bemessung der Schritt-
länge beim graphischen Integrationsverfahren
von Meissner-Ludwig, Verh. Naturforsch.
Ges. Basel 65,
49-66.
- Über eine Klasse von linearen Systemen mit konstanten
Koeffizienten, Comment. Math.
Helv. 28, 186-196.
1955
- Über den Fehler des Runge-Kutta-Verfahrens für die numerische
Integration gewöhn-
licher Differentialgleichungen n-ter
Ordnung, Z. Angew. Math. Phys. 6, 456-461.
1956
- Una estensione agli integrali doppi di una condizione di Picone
necessaria per un estremo, Atti Accad. Naz. Lincei. Rend. Cl. Sci. Fis. Mat. Nat. (8)
20, 283-289.
- Bemerkung zu einer notwendigen Bedingung von Picone in der
Variationsrechnung, Comment. Math. Helv. 31, 1-4.
- (with F. Malmborg) Calculations related to the improved
free-volume-theory of liquids (AF Problem 116), Harvard Computation
Laboratory, Problem Report 100, VI-1-VI-41.
1959
- Some elementary inequalities relating to the gamma and incomplete
gamma function, J. Math. and Phys. 38, 77-81.
- Exponential integral
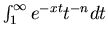 for
large values of n, J. Res. Nat. Bur. Standards 62,
123-125.
for
large values of n, J. Res. Nat. Bur. Standards 62,
123-125.
- Note on bivariate linear interpolation for analytic functions,
Math. Tables Aids Comput. 13, 91-96.
1961
- Recursive computation of certain integrals, J. Assoc. Comput. Mach. 8,
21-40.
- Recursive computation of the repeated integrals of the error
function, Math. Comp. 15, 227-232.
- Numerical integration of ordinary differential equations based on
trigonometric polynomials, Numer. Math. 3, 381-397.
1962
- (with H. A. Antosiewicz) Numerical methods in ordinary
differential equations, Ch. 9 in Survey of numerical analysis
(J. Todd, ed.), 314-346, McGraw-Hill, New York.
- On inverses of Vandermonde and confluent Vandermonde matrices,
Numer. Math. 4, 117-123.
- Diffusion functions for small argument, SIAM Rev. 4,
227-229.
1963
- Instability of linear second-order difference equations, in
Proc. IFIP Congress 62 (C. M.
Popplewell, ed.), 207, North-Holland,
Amsterdam.
- On inverses of Vandermonde and confluent Vandermonde matrices II,
Numer. Math. 5, 425-430.
1964
- (with W. F. Cahill) Exponential integral and related functions,
Ch. 5 in Handbook of mathematical functions (M. Abramowitz
and I. A. Stegun, eds.), 227-251, Nat. Bur.
Standards Appl. Math. Ser. 55.
[Russian translation by V. A. Ditkin and L. N. Karmazina,
in Spravocnik po special'nym funkciyam, 55-79, Nauka,
Moscow, 1979.]
- Error function and Fresnel integrals, Ch. 7 in Handbook of
mathematical functions (M. Abramowitz and I. A. Stegun, eds.),
295-329, Nat. Bur. Standards Appl. Math. Ser.
55.[Russian
translation by V. A. Ditkin and L. N. Karmazina, in Spravocnik
po special'nym funkciyam, 119-152, Nauka, Moscow, 1979.]
- Algorithm 221 -- Gamma function, and Algorithm 222 -- Incomplete
beta function ratios, Comm. ACM 7, 143-144; Certification
of Algorithm 222, ibid., 244.
1965
- Algorithm 236 -- Bessel functions of the first kind, Comm. ACM
7, 479-480; Certification of Algorithm 236, ibid. 8,
105-106.
- Algorithm 259 -- Legendre functions for arguments larger than one,
Comm. ACM 8, 488-492.
1966
- Computation of transcendental functions by recurrence relations,
in Proc. IFIP Congress 65, v. 2 (W. A. Kalenich, ed.),
485-486, Spartan Books, Washington, D. C.
- Computation of successive derivatives of
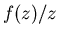 , Math. Comp.
20, 209-214.
, Math. Comp.
20, 209-214.
- Algorithm 282 -- Derivatives of
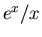 ,
, 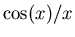 ,
and
,
and 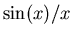 , Comm. ACM 9, 272.
, Comm. ACM 9, 272.
- Algorithm 292 -- Regular Coulomb wave functions, Comm. ACM
9, 793-795.
1967
- Computational aspects of three-term recurrence relations, SIAM
Rev. 9, 24-82.
- Numerical quadrature in the presence of a singularity, SIAM J. Numer. Anal.
4, 357-362.
1968
- Construction of Gauss-Christoffel quadrature formulas, Math. Comp.
22, 251-270.
- Algorithm 331 -- Gaussian quadrature formulas, Comm. ACM 11,
432-436.
1969
- Remark on Algorithm 292, Comm. ACM 12, 280.
- On the condition of a matrix arising in the numerical inversion of
the Laplace transform, Math. Comp. 23, 109-118.
- An application of minimal solutions of three-term recurrences to
Coulomb wave functions, Aequationes Math. 2, 171-176;
abstract, ibid. 1 (1968), 208.
- Algorithm 363 -- Complex error function, Comm. ACM 12,
635.
1970
- (with B. J. Klein) Recursive computation of certain derivatives -- a
study of error propagation, Comm. ACM 13, 7-9.
- (with B. J. Klein) Remark on Algorithm 282, Comm. ACM 13,
53-54.
- Efficient computation of the complex error function, SIAM
J. Numer. Anal. 7, 187-198.
- On the construction of Gaussian quadrature rules from modified
moments, Math. Comp.
24, 245-260.
1971
- Attenuation factors in practical Fourier analysis, Numer. Math. 18,
373-400.
1972
- Zur Numerik rekurrenter Relationen, Computing 9,
107-126.
[English translation in: Aerospace Research Laboratories, Report
ARL 73-0005, February 1973.]
- The condition of orthogonal polynomials, Math. Comp. 26,
923-924.
1973
- Algorithm 471 -- Exponential integrals, Comm. ACM 16,
761-763.
- On the condition of algebraic equations, Numer. Math. 21,
405-424.
1974
- (with H. Yanagiwara) On Chebyshev-type quadratures, Math. Comp. 28,
125-134.
- A harmonic mean inequality for the gamma function, SIAM J. Math. Anal. 5,
278-281.
- Some mean value inequalities for the gamma function, SIAM J. Math. Anal. 5,
282-292.
1975
- Computational methods in special functions -- a survey, in
Theory and applications of special functions (R. A. Askey, ed.),
1-98, Math. Res. Center, Univ. Wisconsin Publ., no. 35,
Academic Press, New York.
- Nonexistence of Chebyshev-type quadratures on infinite intervals,
Math. Comp. 29, 93-99.
- Norm estimates for inverses of Vandermonde matrices, Numer. Math. 23,
337-347.
- Optimally conditioned Vandermonde matrices, Numer. Math. 24,
1-12.
- (with L. A. Anderson) Optimal weighted Chebyshev-type quadrature
formulas, Calcolo 12, 211-248.
- Stime dell'errore globale nei metodi ``one-step'' per equazioni
differenziali ordinarie, Rend. Mat. (2) 8, 601-617.
1976
- Advances in Chebyshev quadrature, in Numerical analysis
(G. A. Watson, ed.), 100-121, Lecture Notes Math., v. 506, Springer,
Berlin.
- Comportement asymptotique des coefficients dans les formules
d'intégration d'Adams, de Störmer et de Cowell, C. R. Acad. Sci. Paris
Ser. A-B 283, A787-A788.
- Qualche contributo recente sul problema di Chebyshev nella teoria
dell'integrazione numerica, Rend. Sem. Mat. Univ. e Politec. Torino
35, 39-44.
1977
- (with G. Monegato) On optimal Chebyshev-type quadratures,
Numer. Math. 28, 59-67.
- Evaluation of the repeated integrals of the coerror function, ACM
Trans. Math. Software 3, 240-252.
- Algorithm 521 -- Repeated integrals of the coerror function, ACM
Trans. Math. Software 3, 301-302.
- Anomalous convergence of a continued fraction for ratios of Kummer
functions, Math.
Comp. 31, 994-999.
1978
- On inverses of Vandermonde and confluent Vandermonde matrices III,
Numer. Math. 29, 445-450.
- (with J. Slavik) On the computation of modified Bessel function
ratios, Math. Comp. 32, 865-875.
- Questions of numerical condition related to polynomials, in
Symposium on recent advances in numerical analysis (C. de Boor and
G. H. Golub, eds.), 45-72, Academic Press, New York.
[Revised and reprinted in MAA Studies in Mathematics, v. 24:
Studies in numerical analysis
(G. H. Golub, ed.), 140-177, Math. Assoc. America, Washington, DC, 1984.]
1979
- On generating Gaussian quadrature rules, in Numerische
Integration (G. Hämmerlin, ed.), 147-154, Internat. Ser. Numer. Math.,
v. 45, Birkhäuser, Basel.
- The condition of polynomials in power form, Math. Comp. 33,
343-352.
- On the preceding paper ``A Legendre polynomial integral'' by James
L. Blue, Math.
Comp. 33, 742-743.
- A computational procedure for incomplete gamma functions, ACM
Trans. Math. Software 5, 466-481.
- Algorithm 542 -- Incomplete gamma functions, ACM Trans. Math. Software
5, 482-489.
- Un procedimento di calcolo per le funzioni gamma incomplete,
Rend. Sem. Mat. Univ. e Politec. Torino 37, 1-9.
- Families of algebraic test equations, Calcolo 16,
383-398.
1980
- (with F. Costabile) Stime per difetto per gli zeri più grandi
dei polinomi ortogonali, Boll. Un. Mat. Ital. (5) 17A,
516-522.
- (with M. Montrone) Metodi multistep con minimo coefficiente
dell'errore globale, Calcolo 17, 67-75.
1981
- A survey of Gauss-Christoffel quadrature formulae, in E. B. Christoffel -- the
influence of his work in mathematics and the
physical sciences (P. L. Butzer and F. Fehér, eds.),
72-147, Birkhäuser, Basel.
- Minimal solutions of three-term recurrence relations and
orthogonal polynomials, Math.
Comp. 36, 547-554.
- Recognition of Christoffel's work on quadrature during and after
his lifetime, in E. B.
Christoffel -- the influence of his
work in mathematics and the physical sciences (P. L. Butzer and F. Fehér,
eds.), 724-727, Birkhäuser, Basel.
1982
- An algorithmic implementation of the generalized Christoffel
theorem, in Numerical integration (G. Hämmerlin, ed.),
89-106, Internat. Ser. Numer. Math., v. 57, Birkhäuser, Basel.
- (with R. E. Lynch) Error behavior in optimal relaxation methods,
Z. Angew. Math. Phys.
33, 24-35.
- A note on the successive remainders of the exponential series,
Elem. Math. 37, 46-49.
- Polynomials orthogonal with respect to the reciprocal gamma
function, BIT 22, 387-389.
- On generating orthogonal polynomials, SIAM J. Sci. Statist. Comput. 3,
289-317.
1983
- To Alexander M. Ostrowski on his ninetieth birthday, Linear
Algebra Appl. 52/53, xi-xiv.
- The condition of Vandermonde-like matrices involving orthogonal
polynomials, Linear Algebra Appl. 52/53, 293-300.
- How and how not to check Gaussian quadrature formulae, BIT
23, 209-216.
- (with R. S. Varga) Error bounds for Gaussian quadrature of
analytic functions, SIAM J. Numer. Anal. 20, 1170-1186.
- On Padé approximants associated with Hamburger series, Calcolo
20, 111-127.
- On the convergence behavior of continued fractions with real
elements, Math. Comp. 40, 337-342.
1984
- (with G. V. Milovanovic) On a class of complex polynomials
having all zeros in a half circle, in Numerical methods and
approximation theory (G. V. Milovanovic, ed.), 49-53, Faculty
of Electronic Engineering, Univ. Niš, Niš.
- Discrete approximations to spherically symmetric distributions,
Numer. Math. 44, 53-60.
- On some orthogonal polynomials of interest in theoretical
chemistry, BIT 24, 473-483.
- (with Jet Wimp) In memoriam YUDELL L. LUKE June 26, 1918 - May 6,
1983, Math. Comp. 43, 349-352.
1985
- Some new applications of orthogonal polynomials,
in Polynômes orthogonaux et applications
(C. Brezinski, A. Draux, A. P. Magnus, P. Maroni and A. Ronveaux, eds.), 63-73,
Lecture Notes Math., v. 1171, Springer, Berlin.
- (with G. V. Milovanovic) Gaussian quadrature involving Einstein
and Fermi functions with an application to summation of series,
Math. Comp. 44, 177-190.
Supplement, ibid., S1-S11.
- Orthogonal polynomials -- constructive theory and applications,
J. Comput. Appl. Math.
12/13, 61-76.
- (with G. V. Milovanovic) Polynomials orthogonal on the
semicircle, Rend. Sem. Mat.
Univ. e Politec. Torino,
Special Issue, 179-185.
1986
- (with B. Flury) An algorithm for simultaneous orthogonal
transformation of several positive definite matrices to nearly
diagonal form, SIAM J. Sci. Statist. Comput. 7, 169-184.
- (with G. V. Milovanovic) Polynomials orthogonal on the
semicircle, J. Approx. Theory 46, 230-250.
- On the sensitivity of orthogonal polynomials to perturbations in
the moments, Numer. Math. 48, 369-382.
- (with F. Caliò and E. Marchetti) On computing Gauss-Kronrod
quadrature formulae, Math. Comp. 47, 639-650.
- (with G. V. Milovanovic) Spline approximations to spherically
symmetric distributions, Numer. Math. 49, 111-121.
- Reminiscences of my involvement in de Branges's proof of the
Bieberbach conjecture, in The Bieberbach conjecture
(Albert Baernstein II, David Drasin, Peter Duren, and Albert Marden, eds.),
205-211, Proc. Symp. on the Occasion of the Proof, Math. Surveys Monographs,
no. 21, American Mathematical Society, Providence, RI.
1987
- (with M. Frontini and G. V. Milovanovic)
Moment-preserving spline approximation on finite intervals,
Numer. Math. 50, 503-518.
- (with J. Wimp)
Computing the Hilbert transform of a Jacobi weight function,
BIT 27, 203-215.
- (with H. J. Landau and G. V. Milovanovic)
Polynomials orthogonal on the semicircle II, Constructive Approx. 3,
389-404.
- (with M. A. Kovacevic and G. V. Milovanovic)
The numerical evaluation of singular integrals with coth-kernel,
BIT 27, 389-402.
- A conjectured inequality for Hermite interpolation at the zeros of
Jacobi polynomials, Problem 87-7, SIAM Rev. 29, 297-298.
1988
- Gauss-Kronrod quadrature -- a survey, in
Numerical methods and approximation theory III
(G. V. Milovanovic, ed.), 39-66, Faculty of Electronic Engineering,
Univ. Niš, Niš.
- (with S. E. Notaris)
Newton's method and Gauss-Kronrod quadrature, in
Numerical integration III
(H. Brass and G. Hämmerlin, eds.), 60-71, Internat. Ser. Numer. Math.,
v. 85, Birkhäuser, Basel.
- (with S. E. Notaris)
An algebraic study of Gauss-Kronrod quadrature formulae for Jacobi
weight functions, Math. Comp. 51, 231-248.
- (with G. Inglese)
Lower bounds for the condition number of Vandermonde matrices,
Numer. Math. 52, 241-250.
- (with T. J. Rivlin)
A family of Gauss-Kronrod quadrature formulae, Math. Comp. 51,
749-754.
1989
- Orthogonality -- conventional and unconventional -- in
numerical analysis, in Computation and control
(K. Bowers and J. Lund, eds.), 63-95, Progress in Systems and
Control Theory, v. 1, Birkhäuser, Boston.
- On the zeros of polynomials orthogonal on the semicircle,
SIAM J. Math. Anal. 20, 738-743.
- (with S. E. Notaris)
Gauss-Kronrod quadrature formulae for weight functions of
Bernstein-Szegö type, J. Comput. Appl. Math. 25,
199-224. [Erratum, ibid. 27 (1989), 429.]
1990
- Some applications and numerical methods for orthogonal polynomials,
in Numerical analysis and mathematical modelling (A. Wakulicz,
ed.), 7-19, Banach Center Publications, v. 24, PWN Polish Scientific
Publishers, Warsaw.
- Orthogonal polynomials on the semicircle, in Numerical
analysis and mathematical modelling (A. Wakulicz, ed.), 21-27, Banach Center
Publications, v 24, PWN Polish Scientific Publishers, Warsaw.
- Computational aspects of orthogonal polynomials, in
Orthogonal polynomials (Paul Nevai, ed.),
181-216, NATO ASI Series, Series C: Mathematical and Physical
Sciences, v. 294, Kluwer, Dordrecht.
- How (un)stable are Vandermonde systems?, in Asymptotic and
computational analysis (R. Wong, ed.), 193-210, Lecture Notes Pure
Appl. Math., v. 124, Dekker, New York.
- (with E. Tychopoulos and R.S. Varga)
A note on the contour integral representation of the remainder term
for a Gauss-Chebyshev quadrature rule, SIAM J. Numer. Anal. 27,
219-224.
- (with A. Córdova and S. Ruscheweyh)
Vandermonde matrices on the circle: spectral properties and
conditioning, Numer. Math. 57, 577-591.
- (with Shikang Li) The remainder term for analytic functions of
Gauss-Radau and Gauss-Lobatto quadrature rules with multiple end
points, J. Comput. Appl. Math. 33, 315-329.
1991
- Computational problems and applications of orthogonal polynomials,
in Orthogonal polynomials and their applications (C. Brezinski,
L. Gori and A. Ronveaux, eds.), 61-71, IMACS Annals Comput. Appl. Math.,
v. 9, Baltzer, Basel.
- On the remainder term for analytic functions of Gauss-Lobatto and
Gauss-Radau quadratures, Rocky Mountain J. Math. 21,
209-226.
- A class of slowly convergent series and their summation by Gaussian
quadrature, Math. Comp. 57, 309-324.
- On certain slowly convergent series occurring in plate contact
problems, Math. Comp. 57, 325-338.
- (with Shikang Li) Gauss-Radau and Gauss-Lobatto quadratures with
double end points, J. Comput. Appl. Math. 34, 343-360.
- On the paper ``A continued fraction approximation of the modified
Bessel function
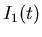 '' by P .R. Parthasarathy and
N. Balakrishnan, Appl. Math. Letters 4, 47-51.
'' by P .R. Parthasarathy and
N. Balakrishnan, Appl. Math. Letters 4, 47-51.
- Quadrature formulae on half-infinite intervals, BIT 31,
438-446.
1992
- Remainder estimates for analytic functions, in Numerical
integration (T. O. Espelid
and A. Ganz, eds.), 133-145, NATO ASI Series, Series C: Mathematical and
Physical Sciences, v. 357, Kluwer, Dordrecht.
- Applications and computation of orthogonal polynomials,
Proc. Eighteenth South African Sympos. Numer. Math. (S. Abelman, ed.),
47-71, Department of Computer Science, University of Natal, Durban.
- Spline approximation and quadrature formulae, Atti Sem. Mat. Fis. Univ. Modena
40, 169-182.
- On mean convergence of extended Lagrange interpolation, J. Comput. Appl. Math. 43,
19-35.
1993
- The spiral of Theodorus, special functions, and numerical
analysis, Supplement A in Spirals: from Theodorus to chaos by
P. J. Davis, 67-87, A K Peters, Boston.
- (with Shikang Li) A set of orthogonal polynomials induced by a
given orthogonal polynomial, Aequationes Math. 46,
174-198.
- Is the recurrence relation for orthogonal polynomials always
stable?, BIT 33, 277-284.
- On the computation of generalized Fermi-Dirac and Bose-Einstein
integrals, Comput. Phys. Comm. 74, 233-238.
- Gauss-type quadrature rules for rational functions, in
Numerical integration IV (H. Brass and G. Hämmerlin, eds.),
111-130, Internat. Ser. Numer. Math., v.112, Birkhäuser, Basel.
- (with S. E. Notaris) Problem 6, in Numerical integration IV
(H. Brass and G. Hämmerlin, eds.), 379-380, Internat. Ser. Numer. Math.,
v. 112, Birkhäuser, Basel.
1994
- Summation of slowly convergent series, in Numerical analysis
and mathematical modelling (A. Wakulicz, ed.), 7-18, Banach Center
Publications, v. 29, PWN Polish Scientific Publishers,
Warsaw.
- Applications and computation of orthogonal polynomials, in
Advances in computational mathematics: New Delhi, India
(H. P. Dikshit and C. A. Micchelli, eds.), Series in Approximations and
Decompositions, v. 4, World Scientific, Singapore.
- Algorithm 726: ORTHPOL -- a package of routines for generating
orthogonal polynomials and Gauss-type quadrature rules,
ACM Trans. Math. Software 20, 21-62; Remark on Algorithm 726,
ibid. 24 (1998), 355.
- Reflections and recollections, in Approximation and
computation: a festschrift in honor of Walter Gautschi (R. V. M. Zahar,
ed.), xvii-xxxv, Internat. Ser. Numer. Math., v. 119, Birkhäuser,
Basel.
1995
- The work of Philip Rabinowitz on numerical integration,
Numer. Algorithms 9, 199-222.
- Luigi Gatteschi's work on special functions and numerical
analysis, Annals Numer.
Math. 2, 3-19.
- (with M. Zhang) Computing orthogonal polynomials in Sobolev
spaces, Numer. Math. 71, 159-183.
1996
- Orthogonal polynomials: applications and computation, Acta
Numerica 1996 (A. Iserles, ed.), 45-119, Cambridge University Press,
Cambridge.
- (with Shikang Li) On quadrature convergence of extended Lagrange
interpolation, Math.
Comp. 65, 1249-1256.
- (with S. E. Notaris) Stieltjes polynomials and related quadrature
formulae for a class of weight functions, Math. Comp. 65,
1257-1268.
1997
- (with J. Waldvogel) Contour plots of analytic functions,
Ch. 25 in Solving problems in scientific computing using Maple
and Matlab (W. Gander and J. Hrebícek, eds.), 3d ed.,
359-372, Springer, Berlin. [Chinese translation by
China Higher Education Press and Springer, 1999; Portuguese
translation of 3d ed. by Editora Edgard Blücher Ltda, Sao Paolo, 2001;
Russian translation of 4th ed. by
Vassamedia, Minsk, Bjelarus, 2005.]
- The computation of special functions by linear difference
equations, in Advances in difference equations (S. Elaydi,
I. Gyori, and G. Ladas, eds.), 213-243, Gordon and Breach, Amsterdam.
- On the computation of special Sobolev-type orthogonal polynomials,
The heritage of P. L. Chebyshev: a festschrift in honor of the 70th
birthday of T. J. Rivlin, Ann. Numer. Math. 4, 329-342.
- Moments in quadrature problems, Approximation theory and
approximation, Comput. Math. Appl. 33, 105-118.
- (with A. B. J. Kuijlaars) Zeros and critical points of Sobolev
orthogonal polynomials, J. Approx. Theory 91, 117-137.
- (with G. V. Milovanovic) s-orthogonality and construction of
Gauss-Turán-type quadrature formulae, J. Comput. Appl. Math. 86,
205-218.
1998
- The incomplete gamma functions since Tricomi, in Tricomi's
ideas and contemporary applied mathematics, 203-237, Atti dei Convegni Lincei,
n. 147, Accademia Nazionale dei Lincei, Roma.
- Ostrowski and the Ostrowski prize, Math. Intelligencer 20,
32-34. [Revised and translated into German, Uni Nova 87 (2000),
60-62, Universität Basel.]
1999
- Orthogonal polynomials and quadrature, Electron. Trans. Numer. Anal. 9,
65-76.
- A note on the recursive calculation of incomplete gamma
functions, ACM Trans. Math.
Software 25, 101-107.
- Algorithm 793: GQRAT -- Gauss quadrature for rational functions,
ACM Trans. Math.
Software 25, 213-239.
2000
- (with W. Gander) Adaptive quadrature -- revisited, BIT 40,
84-101.
- (with L. Gori and F. Pitolli) Gauss quadrature for refinable
weight functions, Appl. Comput. Harmon. Anal. 8,
249-257.
- (with L. Gori and M. L. Lo Cascio) Quadrature rules for rational
functions, Numer. Math. 86, 617-633.
- High-order Gauss-Lobatto formulae, Numer. Algorithms 25, 213-222.
- Gauss-Radau formulae for Jacobi and Laguerre weight functions,
Math. Comput. Simulation 54, 403-412. [Reprinted
in Computational Science, Mathematics and Software
(Ronald F. Boisvert and Elias Houstis, eds.), 237-248, Purdue University
Press, West Lafayette, IN.]
2001
- Remark on the paper ``Barycentric formulae for cardinal (SINC-)
interpolants'' by Jean-Paul Berrut, Numer. Math. 87,
791-792.
- (with J. Waldvogel) Computing the Hilbert transform of the
generalized Laguerre and Hermite weight functions, BIT 41,
490-503.
- The use of rational functions in numerical quadrature,
J. Comput. Appl. Math. 133, 111-126.
2002
- Gauss quadrature approximations to hypergeometric and
confluent hypergeometric functions, J. Comput. Appl. Math. 139,
173-187.
- Computation of Bessel and Airy functions and of
related Gaussian quadrature formulae, BIT 42,
110-118.
- The interplay between classical analysis and
(numerical) linear algebra -- a tribute to Gene H. Golub,
Electron. Trans. Numer. Anal. 13,
119-147.
- Alessandro M. Ostrowski (1893-1986). La sua vita
e le opere, Boll. Docenti Matem. 45, 9-19.
2003
- (with F. E. Harris and N. M. Temme) Expansions of the
exponential integral in incomplete gamma functions,
Appl. Math. Lett. 16, 1095-1099.
2004
- Generalized Gauss-Radau and Gauss-Lobatto formulae,
BIT 44, 711-720.
2005
- Orthogonal polynomials (in Matlab), J. Comput. Appl. Math. 178,
215-234.
- The Hardy-Littlewood function: an exercise
in slowly convergent series, J. Comput.
Appl. Math. 179,
249-254.
- Computing polynomials orthogonal with respect to densely
oscillating and exponentially decaying weight functions and
related integrals, J. Comput. Appl. Math. 184,
493-504.
- A historical note on Gauss-Kronrod quadrature,
Numer. Math. 100, 483-484.
- Numerical quadrature computation of the Macdonald
function for complex orders, BIT Numer. Math. 45,
593-603.
2006
- Orthogonal polynomials, quadrature, and approximation:
computational methods and software (in Matlab), in
Orthogonal polynomials and special functions -- computation
and applications (Francisco Marcellán and Walter Van Assche, eds.),
1-77, Lecture Notes Math. 1883.
- The circle theorem and related theorems for
Gauss-type quadrature rules, Electron. Trans.
Numer. Anal. 25,
129-137.
- Computing the Kontorovich-Lebedev integral
transforms and their inverses, BIT Numer. Math. 46,
21-40.
2007
- (with Paul Leopardi) Conjectured inequalities for
Jacobi polynomials and their largest zeros, Numer. Algorithms
45, 217-230.
- Leonhard Eulers Umgang mit langsam konvergenten
Reihen, Elem. Math. 62, 174-183.
- Commentary, in Milestones in matrix
computation: selected works of Gene H. Golub, with
commentaries (Raymond H. Chan, Chen Greif, and Dianne P. O'Leary, eds.),
345-358, Oxford University Press, New York.
- A guided tour through my bibliography, Numer. Algorithms
45, 11-35.
2008
- On Euler's attempt to compute logarithms by
interpolation: a commentary to his letter of
February 16, 1734 to Daniel Bernoulli,
J. Comput. Appl. Math. 219, 408-415.
- Leonhard Euler: his life, the man, and his work,
SIAM Rev. 50, 3-33. [Also published in
ICIAM 07,
 International Congress on
Industrial and Applied Mathematics, Zürich, Switzerland,
16-20 July 2007 (Rolf Jeltsch and Gerhard Wanner, eds.),
447-483, European Mathematical Society, 2009. Chinese
translation in Mathematical Advance in Translation
(2008)(2-3).]
International Congress on
Industrial and Applied Mathematics, Zürich, Switzerland,
16-20 July 2007 (Rolf Jeltsch and Gerhard Wanner, eds.),
447-483, European Mathematical Society, 2009. Chinese
translation in Mathematical Advance in Translation
(2008)(2-3).]
- The numerical evaluation of a ``challenging'' integral,
Numer. Algorithms 49, 187-194.
- (with Carla Giordano) Luigi Gatteschi's work on asymptotics of special
functions and their zeros, Numer. Algorithms 49,
11-31.
- On a conjectured inequality for the largest zero of
Jacobi polynomials, Numer. Algorithms 49,
195-198.
2009
- On conjectured inequalities for zeros of Jacobi
polynomials, Numer. Algorithms 50, 93-96.
- New conjectured inequalities for zeros of Jacobi
polynomials, Numer. Algorithms 50,
293-296.
- How sharp is Bernstein's inequality for Jacobi
polynomials?, Electr. Trans. Numer. Anal.
36,
1-8.
- High-order generalized Gauss-Radau and Gauss-Lobatto
formulae for Jacobi and Laguerre weight functions,
Numer. Algorithms 51, 143-149.
- Variable-precision recurrence coefficients for nonstandard
orthogonal polynomials, Numer. Algorithms 52,
409-418.
2010
- Alexander M. Ostrowski (1893-1986): his life, work, and
students, in math.ch/100 Swiss Mathematical
Society 1910-2010 (Bruno Colbois, Christine Riedtmann,
and Viktor Schroeder, eds.), 257-278, European Mathematical
Society.
- The spiral of Theodorus, numerical analysis, and special
functions, J. Comput. Appl.
Math. 235, 1042-1052.
- Gauss quadrature routines for two classes of logarithmic
weight functions, Numer. Algorithms 55,
265-277.
2011
- The Lambert W-functions and some of their integrals: a case
study of high-precision computation, Numer. Algorithms 57,
27-34.
- Optimally scaled and optimally conditioned Vandermonde and
Vandermonde-like matrices, BIT Numer. Math. 51, 103-125.
- My collaboration with Gradimir V. Milovanovic,
in Approximation and computation -- in honor of Gradimir
V. Milovanovic (Walter Gautschi, Giuseppe Mastroianni, and
Themistocles M. Rassias, eds.), 33-43, Springer Optim. Appl., v. 42,
Springer, Dordrecht.
- Experimental mathematics involving orthogonal polynomials,
in Approximation and computation -- in honor of Gradimir
V. Milovanovic (Walter Gautschi, Giuseppe Mastroianni, and
Themistocles M. Rassias, eds.), 115-131, Springer Optim. Appl.,
v. 42, Springer, Dordrecht.
- Remark on ``New conjectured inequalities for zeros of Jacobi
polynomials'' by Walter Gautschi, Numer. Algorithms 50: 293-296
(2009), Numer. Algorithms 57, 511.
2012
- Numerical integration over the square in the presence of
algebraic/logarithmic singularities with an application to
aerodynamics, Numer. Algorithms 61, 275-290.
- Sub-range Jacobi polynomials, Numer. Algorithms 61,
649-657.
- Interpolation before and after Lagrange, Rend. Sem. Matem. Univ. Politecn. Torino
70, 347-368.
2013
- Repeated modifications of orthogonal polynomials
by linear divisors, Numer. Algorithms 63, 369-383.
- Neutralizing nearby singularities in numerical quadrature,
Numer. Algorithms 64, 417-425.
2014
- High-precision Gauss-Turán quadrature rules for
Laguerre and Hermite weight functions, Numer. Algorithms
67, 59-72.
- A brief summary of my scientific work and highlights of
my career, in Walter Gautschi--selected works with
commentaries, Vol. 1 (C. Brezinski and A. Sameh, eds.), 9-17,
Birkhäuser, Boston, MA.
2015
- Polynomials orthogonal with respect to exponential
integrals, Numer. Algorithms 70, 215-226.
2016
- Algorithm 957: Evaluation of the repeated integrals of
the coerror function by half-range Gauss-Hermite quadrature,
ACM Trans. Math. Software 42, 9.1-9.10.
- Kommentar zum Brief Leonhard Eulers an Daniel Bernoulli vom
27. Februar 1734, Opera Omnia IVA/3, p. 116, Birkhäuser, Basel.
2017
- Monotonicity properties of the zeros of Freud and
sub-range Freud polynomials: analytic and empirical results,
Math. Comp. 86, 855-864.
- Erratum to: Sub-range Jacobi polynomials, Numer. Algorithms 74, 637.
- Polynomials orthogonal with respect to cardinal B-spline weight
functions, Numer. Algorithms 76, 1099-1107.
- A discrete top-down Markov problem in approximation theory, in
Frontiers in orthogonal polynomials and q-series (Xin Li and
Z. Nashed, eds.), World Scientific Publishers, to appear.
- On the Ismail-Letessier-Askey monotonicity conjecture for zeros
of ultraspherical polynomials, in Frontiers in orthogonal
polynomials and q-series (Xin Li and Z. Nashed, eds.), World Scientific
Publishers, to appear.


Next: Mathematical Software
Up: VITA WALTER GAUTSCHI
Previous: Translations
Walter Gautschi
2017-11-27