Donald B. Wagner (University of Copenhagen) has concluded that the third-century Chinese commentator Liu Hui gave a dissection proof of the Pythagorean theorem. His conclusion appears in "A proof of the Pythagorean Theorem by Liu Hui (third century AD)", Historia Mathematica 12 (1985), pp. 71-73. Since the diagram to which Liu Hui refers is no longer extant, the conclusion is based on the wording on page 241 in Qian Baocong (ed.), 1963, Suanjing shi shu [Ten mathematical classics], Beijing: Zhonghua shuju.
More discussion on this theory has been put forward by Karine Chemla, in "Geometrical Figures and Generality in Ancient China and Beyond: Liu Hui and Zhao Shuang, Plato and Thabit ibn Qurra", Science in Context 18(1) (2005), pp. 123-166. The author performs an extensive analysis of the role of visual aids in the mathematical proofs in ancient Chinese manuscripts. She points out parallels between two Chinese texts dealing with the Pythagorean theorem and the figure-based demonstrations of Plato(in the Menon) and Thabit.
The University of Michigan has made available an electronic copy of Paul Mahlo's 1908 dissertation.
Bill Casselman (at the University of British Columbia) asked me about the source for Fig. 4.5, which I had neglected to include in the text. The earliest article that I found that contains this figure is "Der Pythagoräische Lehrsatz", by Felix Bernstein (in Göttingen), Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht 55 (1924), pp. 204-207.
In Ernest Freese's diagrams (from the 1950's), which I got access to late in 2002, there is a diagram for a 6-piece dissection of two unequal squares to two different unequal squares. Thus he discovered the dissection in Figure 4.8 at least 40 years before I published my book.
From the paper by Christian Blanvillain and Janos Pach (as discussed in the next entry), I have become aware of an anonymous obituary for Henry Perigal that appeared inProceedings of the London Mathematical Society, series 1, volume 29 (1897-1898), in the appendix, on pages 732-735.Quoting from page 733:"He also displayed great ingenuity in proving geometrical theorems by means of dissection and transposition of parts. These dissections were mostly discovered between 1830 and 1840. Among the best are his proof of Euclid I. 47, and his decomposition of a square into three squares. Unfortunately, nearly all of his work was published merely for private distribution among his friends, and, as he had not the pen of a ready writer (as he himself used to say), his diagrams were generally issued without sufficient explanation, and sometimes without any at all. These fugitive pieces, which were being produced by him for sixty years or more, are very numerous. They consist principally of diagrams of bicircloidal curves (some on large sheets), of the "Lissajous" curves, and of dissections. Some of the dissections he made as puzzles, forming them in card and wood, and gave to friends. He also engraved them (as well as the finite parabola) upon some of his visiting cards. His proof of Euclid I. 47 was reproduced in Vol. II of the Messenger of Mathematics."Thus it is quite possible that the 6-piece dissection of three congruent squares to a larger square, as shown in my Figure 4.11, was discovered by Perigal between 1830 and 1840. That would predate the related discovery by Kelland in 1855. Yet the above account is not precise enough to know for sure, and indeed we do not even know the author of these remarks. (It appears not to be L.J. Rogers, as a reference in Blanvillain and Pach's paper might lead us to believe.)
In June 2010, Christian Blanvillain, a graduate student in Computer Science, and his adviser Janos Pach, at the Ecole Polytechnique Fédérale de Lausanne, Switzerland, released a paper"Square Trisection: Dissection of a square in three congruent partitions,"which describes a lovely new 6-piece dissection of three congruent squares to one. Unlike the earlier 6-piece Perigal/Kelland dissection, the Blanvillain/Pach dissection has 2-fold rotational symmetry. It is also translational. All angles are multiples of 30 degrees, and each edge length of a piece is either 1 or (√3 - 1), where each of the three congruent squares has a sidelength of 1. Each of the congruent squares is cut into 2 pieces. Altogether, it's nifty!
As a further note, Blanvillain and Pach point out that their basic dissection allows for an infinite number of 6-piece variations. While they lose the lovely edge-length property for the other variations, it is possible to choose one in which all pieces have the same area. They illustrate this case in their Figure 37.
I recently gave an improved discussion of Harry Lindgren's Q-slide, which appears in Figure 4.13. In my discussion I overlapped the two quadrilaterals that I was dissecting, which led to a particularly simple way to think of the dissection. Then I recalled an even simpler overlap that I have used to think about a P-slide.
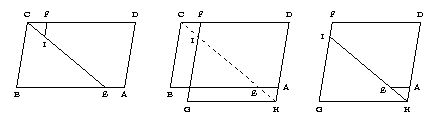
Consider the middle of the figure below, which contains parallelograms ABCD and DFGH, which we would like to dissect one into the other. Note that the parallelograms are positioned so that the points D overlap in each, as do points A and points F.
Now consider the (dashed) edge CH which cuts through both of the overlapping parallelograms. The dissection for each parallelogram is produced from a cut corresponding to the dashed edge, plus a cut resulting from a side of the other parallelogram.
The dissected parallelograms are shown on the right and on the left. Simple, isn't it?

In Figure 4.15, I use two uncentered versions of Perigal's dissection. As it turns out, Arthur W. Siddons noted in "1020. Perigal's Dissection for the Theorem of Pythagoras", Mathematical Gazette, vol. 16, no. 217 (February 1932), p. 44, that uncentered versions of Perigal's dissection exist. His Figure 1 illustrates a case when 5 pieces still suffice, while his Figures 2 and 3 show how additional pieces must be used if the version is too uncentered.
- Thanks to David Singmaster for sending me a copy of Siddons' note.
Near the bottom of page 33, I claim that for the case of dissecting three unequal squares to one, eight pieces always suffice. This is not (yet) true, as Philippe Chevanne, a retired electronics engineer from Paris, France, has pointed out. The problem comes in the case that Figure 4.17 purportedly handles. Well, nothing is wrong with that figure for the specific values of x, y, and z as shown. However, if we take x small enough, with x and y together having large enough area, then we run into problems: Specifically, the diagonal cut for one of the P-slides in Figure 4.17 will be in the way of our cut to relieve the "overlap". And unfortunately, using a strip dissection in place of the P-slide will not help. This is all carefully explained on a webpage of Philippe's.
For the set of values x, y, and z for which Figure 4.17 fails, it is easy to come up with a 9-piece dissection that is derived from the basic method for that figure. Instead of eliminating the overlap by cutting a rectangle out of the z-square, cut a right triangle out of each of the y-square and the z-square, where these right triangles are obtained by a diagonal cut of the rectangle of overlap. Of course, make the cut that produces the right triangles in a way that it is as close as possible to being parallel with the long cuts in the P-slides.
The existence of Theon's class discussed in the updates to chapter 8 suggests a relationship that I missed for three squares to one. The relationship is x (w - x - y) = z (z - w + x) for x < y < z. The resulting 7-piece dissections seem closely related to those for relationship 4.5.
In their 1998 note, "Three Proofs Without Words for the Sine of the Sum," Volker Priebe and Edgar A. Ramos, at the Max-Planck-Institut für Informatik, Saarbrücken, Germany, have found several nice dissection proofs of the addition formula for sines:
sin(α+β) = sin(α) cos(β) + sin(β) cos(α)
Their dissection proofs are generalizations of dissection proofs for the Pythagorean theorem. In place of an x-square and a y-square they have a (sin(α) x cos(β))-rectangle and a (sin(β) x cos(α))-rectangle. In place of the z-square they have an (α+β)-rhombus of sidelength 1. Below on the left is a variation of their second figure, which shows the superposition of tessellations. On the right is the corresponding dissection, which is a generalization of Thabit's dissection. These are analogous to Figures 4.1 and 4.2.
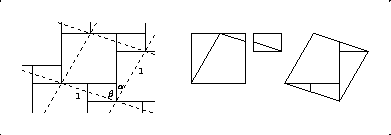
There is also a dissection that is related to Perigal's dissection in the same way that the one by Priebe and Ramos is related to Thabit's dissection. While it is less self-evidently a proof of the addition formula for sines, it is a more symmetric dissection and is even hingeable. The superposition of tessellations and the corresponding dissection below are analogous to Figures 4.5 and 4.6.
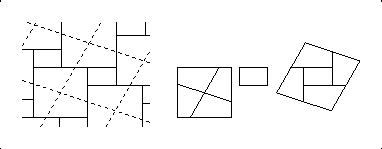
As luck would have it, it is the third proof of Priebe and Ramos that is published in "Proof Without Words: The Sine of a Sum," Mathematics Magazine, volume 73, number 5, December 2000. This one is not based on tessellations, and the (sin(α) x cos(β))-rectangle, (sin(β) x cos(α))-rectangle, and (α+β)-rhombus are not cut, but are left when two right triangles of angle α and two right triangles of angle β are rearranged within a ((sin(α+sin(β))) x (cos(α)+cos(β)))-rectangle.
Erwin Dintzl was not the originator of the tessellation of squares and parallelograms that appears in solid edges in Figures 4.25 and 4.27. Instead, the tessellation is in Figure 10 of "Die regelmässigen ebenen Punktsysteme von unbegrenzter Ausdehnung," by Leonhard Sohncke, of Carlsruhe, in Journal für die reine und angewandte Mathematik (Crelle's Journal), volume 77, first part, 1873.
Günter Rote has pointed out that a "Promotion" is the act by which a doctoral degree is bestowed, and also the associated academic ceremony. So Erwin Dintzl would have been awarded a Dr. phil.
(This is corrected in the paperback edition.)
Copyright 1997-2014, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print a copy
of this page for his or her own personal use.
Last updated June 6, 2014.