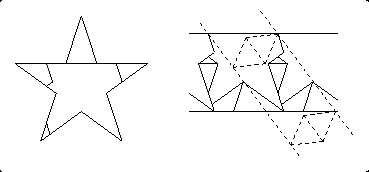
In May 1999 Gavin Theobald improved by one piece his earlier 11-piece dissection of a pentagram to a hexagram. I did not include his earlier dissection in my book, since it used strips that he had employed for other dissections in my book. However, he has created a new pentagram strip for this dissection, so I would like to illustrate it here.

To get the strip element, Gavin cut the pentagram into five pieces, rather than the four of Fig. 11.24 or Fig. 12.22. The resulting strip accommodates cross-strips that are somewhat narrow. Gavin found that this strip gives dissections that tie previous results in a few cases, but only for the dissection to a hexagram is there an improvement. With just 10 pieces for one star to the other, this is a nifty dissection. Note that the boundary of the hexagram strip does not go through the lower crotch of the pentagram, but slightly to the right of it.
I missed some of the history relating to the pentagram to square dissection. In 1958 Martin Gardner had proposed as a problem (E1309) in the American Mathematical Monthly finding a dissection of a pentagram to a square in at most nine pieces. (Thus we may assume that Martin had a 9-piece solution.) Harry Lindgren's 8-piece dissection was given as the solution, but T. Bakos and E. R. Herbst also gave 8-piece dissections.
And slightly earlier: In Ernest Freese's manuscript, Geometric Transformations (completed before his death in 1957), which I got access to in February 2003, there is (in Plate 59) a 9-piece dissection.
Alain Rousseau pointed out a mistake in my discussion on the T-slide in the first full paragraph of page 130. The third and fourth sentences should be corrected to read:Next we locate point G on CD so that the sum of the lengths of BE and GC equals the length of AE. Finally, we let point F be the midpoint of DG and H the midpoint of BC.(This is corrected in the paperback edition.)
On page 130, I stated that the T-slide converts a trapezoid to a parallelogram. Actually, the T-slide is a bit more general, converting a trapezoid to another trapezoid, where the trapezoids have one angle the same.
The caption to Figure 11.38 should read "hexagons", not "hectagons".
(This is corrected in the paperback edition.)
After discussing Gavin Theobald's wonderful 7-piece dissection of a decagon to a square, I referenced Harry Lindgren's (1964b) 8-piece dissection. But that had appeared earlier in (Lindgren 1962a). In addition, Ernest Irving Freese had found even earlier an 8-piece dissection, as discussed in (Lindgren 1964b).
In January 2014, Gavin Theobald improved on his 8-piece dissection of an octagon to a hexagon, shown in Figure 11.39. He has now found a 7-piece dissection, with two pieces turned over. The resulting dissection would no longer fit in Chapter 11, because it results from superposing two tessellations, one for hexagons and the other for octagons. The tessellations are special-purpose ones, designed to work well with each other.
Gavin Theobald sent me his dissections just a few months before a final version of my manuscript was due at the publisher. In addition, I was running up against the page limit that my publisher had set. So I never had full opportunity to include as many of his dissections as I would have liked. Now you can see a wonderful presentation of many more of Gavin's dissections.
David Paterson recently showed me a clever 14-piece dissection, which he had in fact discovered back in 1985. He converted the hendecagon to a rectangle in 10 pieces and then applied a P-slide.
But in August 2000 this was topped by Gavin Theobald, who found a remarkable 13-piece dissection of a hendecagon to a square. Gavin cut the hendecagon into three pieces, from which he proceeded to make two different strip elements. The creation of each strip element is very clever. Then he used each strip to get a rectangle of length equal to the side of the square. Thus he has what Harry Lindgren called a piecemeal dissection.
In January 2001 Gavin sent me an improvement on this dissection. Instead of producing one of the two rectangles, he produced a parallelogram and cut a portion out of the other rectangle into which it fits. Thus Gavin knocked the number of pieces down to 12. But see a later update!
In August and September of 2000, Gavin Theobald found surprising dissections for a number of many-sided polygons to a square. These included a {16} to a square in 11 pieces, a {14} to a square in 12 pieces (but improved here!), a {13} to a square in 13 pieces, an {18} to a square in 13 pieces, and a {20} to a square in 17 pieces (16 if pieces can be turned over). His approach was to cut these figures into pieces that tessellate the plane. He then converted the tessellation element to a strip element. The tessellations are lovely and nonobvious.
In January 2001, Gavin sent me another dissection in this series. It is of a {15} to a square, in 13 pieces. Well done!
In January 2001, Gavin Theobald sent me another of his remarkable dissections. It is a {54} to a square, in just 25 pieces! He used many of his tricks from the above improved dissections, but the number of pieces is so small in relation to the number of sides, that I am listing this dissection separately.
There are so many sides in a {54} that, on my postscript viewer, it at first looked like Gavin had squared the circle! However, when I printed out his diagram, I could verify that indeed there were 54 sides.
In January 2002, Gavin Theobald sent me an improvement on his earlier 12-piece dissection of a {14} to a square. Now he uses just 10 pieces!
Gavin's technique is to cut the {14} into three pieces that tile the plane. He then cuts a strip out of the tessellation. The strip element is very long and thin, and contains six pieces. He then crossposes a strip of squares with the new strip, so that the area common to both strips is one half the area of the square; he then lines up a second strip parallel to the first to give a common area equal to that of the square. I suppose that Harry Lindgren might have called this a PP(.5) strip dissection. Well done, Gavin!
In September 2003 Gavin made yet another improvement on his hendecagon to square dissection. He found an approach that uses only eleven pieces! One piece was rather tiny, so that Gavin's dissection also leads to a 10-piece approximate dissection. Two days later, Gavin found a different way to do the dissection so as to avoid having a tiny piece in an 11-piece dissection. But see a later update!
In September 2003, Gavin Theobald sent me an improvement on his earlier 13-piece dissection of a {13} to a square. Now he is using just 12 pieces! This came a day after Gavin sent me his improved hendecagon to square. It looks like Gavin is on a roll again!
A day after Gavin Theobald sent me his 12-piece dissection of a {13} to a square, he improved his dissection of a {15} to a square to just 12 pieces! Thus the approach that allowed the recent improvements in the {11} and the {13} to a square (see the previous entry) also apply to the {15}. This is really exciting!
A day after Gavin Theobald sent me his 12-piece dissection of a {15} to a square, he discovered a new dissection, of a {17} to a square. He used a similar approach to his recent dissections of {11}, {13}, and {15} to a square, with the dissection requiring just 14 pieces! Gavin concluded his message:But any further improvements are going to be difficult. I may attempt the dissection of the 19-gon but this will not be easy. Dissections of n-gons for n>18 require rather more pieces. Multiples of 6 are more efficient so the dissection of a 24-gon should be fairly straightforward. Improving any of the other dissections now seems difficult so further progress is likely to be slow. Still, the roll was good while it lasted - three improvements and a new dissection.
A week later, Gavin Theobald came back with a 10-piece dissection of a hendecagon to a square! This was in response to my message:> I think the roll has come to an end!To which he responded:
Tell me it ain't so!I spoke too soon! Here is an improvement for the hendecagon, and I have just found an 11 piece dissection of the pentadecagon, although it needs verifying. The tridecagon dissection currently requires 12 pieces - this is looking a bit high now, so I think that there is an eleven piece dissection waiting to be found.
On Monday morning, Gavin informed me that he had indeed found an 11-piece dissection of a {13} to a square.
The same morning, Gavin informed me that he had indeed found an 11-piece dissection of a {15} to a square, but with three pieces turned over. Still, that's nothing to sneeze at!
The same morning, Gavin informed me that he had indeed found a 13-piece dissection of a {17} to a square. This last set of dissections employ a somewhat common approach, but each must be finetuned with its own set of optimizations. Regarding the latest dissection of a {17} to a square, Gavin wrote:This was not easy to find. Out of 32 possible combinations of strips this was the only one I found that resulted in a 13 piece dissection.
The day after, Gavin sent me a 15-piece dissection of a {20} to a square. This eclipses his earlier 16-piece dissection, which needed to turn over pieces.
After Gavin had started on this recent roll, I mentioned that the only many-sided polygon to a square that Ernest Freese had done but not him was a {24} to one. Very quickly Gavin came up with an amazing 14-piece dissection!
A week later, Gavin was still at it! He sent me a {20} to a square, eclipsing his earlier 15-piece dissection. Gavin wrote:This was definitely a hard one to crack. The problem was to find a dissection where the rectangular section that dissects to the second smaller strip gives a dissection in only three pieces. I only succeeded after finding a new icosagon strip.
Three months after Gavin's last improvement on his dissections of a {17} to a square and a {15} to a square, Gavin is back! Gavin has now reduced the number of pieces from 13 to 12 for the {17} to a square, and from 12 to 11 for the {15} to a square. Wow!
Following quickly upon Gavin's last improvement on his dissections of a {17} to a square and a {15} to a square, Gavin has now applied a similar improvement to his dissection of an {18} to a square. Gavin has now reduced the number of pieces from 13 to 12 for this polygon. At first glance, it looked as though he had gotten the number of pieces down to 11. However, there is a tiny piece, which looks like it will be hard to get rid of.
Two days later, Gavin sent me a 1-piece improvement on his dissection of a {54} to a square. He currently uses 24 pieces, with one of them being tiny. Gavin wrote:24 pieces may seem a lot but the optimal would be 1+3+9 = 13 pieces so there is an 11 piece overhead for what is in effect 3 subdissections - for the 1 large hexagonal piece (5 pieces), the 3 smaller hexagonal pieces (7 pieces) and the 9 tiny hexagonal pieces (12 pieces). So 24 pieces will be very hard to beat.
In theory I can now dissect the 162-gon in 24+27+3 = 54 pieces.
I have often been asked questions such as: Are there any bounds on the minimum number of pieces needed for a given dissection? Is a particular dissection, such as the 4-piece dissection of an equilateral triangle to a square, optimal? Taking the second question first, I know of no proofs of optimality in a general context. For the first question, some answers for dissecting regular polygons to squares and regular polygons to regular polygons are available in:Evangelos Kranakis, Danny Krizanc, and Jorge Urrutia, "Efficient Regular Polygon Dissections," Geometriae Dedicata, vol. 80, 2000, pp. 247-262.Among other things, they show that the number of pieces p(n,4) required by a minimal dissection of an n-sided regular polygon to a square satisfiesn/4 <= p(n,4) <= n/2 +o(n)The notation o(n) means some value that grows more slowly than n.
Looking back at my messages from Gavin Theobald during September 2003, I found one message that indicated that the lower bound of n/4 is not so far off the mark. Gavin wrote:One dissection that I have never got around to producing diagrams for is the 162-gon to a square. This can, I think, be done in just (!) 25+27+3 = 55 pieces. It is very similiar to the 54-gon dissection, except that there are an additional 26 identical small hexagons, a comb with 27 teeth and 3 more piece. The problem is the 26 small hexagons are very small.
Of course, after that there is the 486-gon is 55+81+3 = 139 pieces, the 1404-gon in 139+243+3 = 385 pieces... This approaches n/4 pieces for an n-gon. I wish I had the time to publish these.
In January 2004, Gavin Theobald went to work on two polygons that he had not previously dissected, the {19} and the {21}. For a {19} to a square, he produced a 15-piece dissection that has one piece turned over, and a 16-piece dissection with no pieces turned over. For a {21} to a square, he produced a 14-piece dissection that has one piece turned over, and a 16-piece dissection with no pieces turned over. There seems to be no connection between the piece turned over in one dissection and the piece turned over in the other.
In February 2004, Gavin Theobald took the lessons learned from dissecting many-sided polygons to squares, and went to work on the enneagon once again. The results are a remarkable 10-piece dissection of an enneagon to a pentagon and a remarkable 12-piece dissection of an enneagon to an octagon.
A week later, Gavin sent me improved dissections of an enneagon to a hexagon (10 pieces, with one turned over) and to a Greek cross (11 pieces). Both of these used a similar attack.
And these were quickly followed by a 10-piece enneagon to a Latin cross and a 13-piece enneagon to a heptagon, again exploiting the same basic insight. See them all at Gavin's website.
In March 2004, Gavin Theobald revisited dissections that he had worked on a decade before. First, he attacked the hexagon, using a simple technique to get a family of hexagon tessellations. Using the tessellation, he found an 8-piece dissection of a hexagon and a decagon, with three pieces turned over. Then he produced an 8-piece dissection of an {8/3} to a hexagon, with one piece turned over. This latter dissection is especially remarkable, as four of the pieces are not convex. It's amazing how they just barely pack in together to form either of the two figures.
A week later, Gavin sent me a 9-piece dissection of a pentagon to a decagon. He used the same decagon strip as in his hexagon-decagon dissection. In fact, he had discovered this dissection years ago, but thought that it wasn't correct, because of how close certain line intersections are. See them all at Gavin's website.
In April 2004, Gavin Theobald found a nifty strip element for the {10/4}. From it he produced 10-piece dissections of the {10/4} to the triangle and to the square. (See Gavin's website.) The dissection to the square matches the number of pieces for an unpublished dissection by Anton Hanegraaf. Anton partitioned the star into the same element as Gavin, but then formed a rectangle and applied a Q-slide.
In August 2004, Gavin Theobald revisited the dissection of a {12/2} to a square. Eight years earlier, he had reduced by one piece Robert Reid's 9-piece dissection, but still needed to turn over one piece, as Robert had done. Now he has figured out a clever way to avoid turning over a piece. (See Gavin's website.)
In December 2004, Gavin sent me the diagrams of the related dissection of a {12/2} to a rectangle that is nearly square. This made his method much clearer, although it might still benefit from some additional explanation.
In December 2004, Gavin Theobald tackled the dissections of a {7/2}, a {9/2}, and a {10/2} to a square. He accomplished this using eleven, twelve, and twelve pieces, respectively. These are sophisticated dissections. (See Gavin's website.)
At the end of January 2005, Gavin Theobald sent me an improved dissection of a {10/2} to a square. He reduced the number of pieces to eleven. This is a nifty improvement on an already nifty dissection. (See Gavin's website.)
At the beginning of March 2005, Gavin Theobald sent me a cleaner dissection of an enneagon to a square. The number of pieces is still nine, but now none of them have the very short sidelengths that were a blemish on his dissection in Figure 11.36. (See Gavin's website.)
May 2005 was star-to-square month for Gavin Theobald! He improved his dissection of a {7/2} to a square down to 10 pieces, and his dissection of a {10/2} to a square down to 10 pieces, or 9 with if you turn over one piece. He also produced first ever dissections of a {7/3} to a square (12 pieces), a {9/3} to a square (12 pieces, with three turned over), and a {10/3} to a square (11 pieces). (See Gavin's website.)
In August 2005, Gavin Theobald focused on dissections of {30} to a square and {36} to a square. He found solutions in 16 and 17 pieces, respectively. The latter is with one piece turned over. Both dissections rely on the idea of slicing trapezoids off the sides, producing a decagon and a dodecagon, resp. He thus adapted the familiar dissections of a decagon to a square and a dodecagon to a square, first dissecting to rectangles and then adding in the trapezoids and converting to squares in the process (See Gavin's website.)
In October 2005, Gavin Theobald improved the dissections of a {36} to a square, to 17 pieces, with no pieces turned over, to 16 pieces, with one piece turned over. (See Gavin's website.)
In May 2007, Gavin Theobald produced a number of nifty dissections involving {8/2} and {12/2}. These include(See Gavin's website.)
- {6/2} to {8/2} in 11 pieces
- {7} to {12/2} in 11 pieces
- {8} to {8/2} in 11 pieces
- {8} to {12/2} in 12 pieces
- {8/2} to {12/2} in 13 pieces
- {5/2} to {12/2} in 14 pieces
Images of Gavin Theobald's dissections are reproduced with his permission.
(Thanks, Gavin!)
All other material is copyright 1997-2007, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print out a copy
of this page for his or her own personal use.
Last updated May 25, 2007.