We would like to propose a novel uniform approach to various data media such as text, image, video and audio based on an approximate pattern matching. This novel time-domain approach is being developed by us at Purdue. We propose to call it PMMC ( Pattern Matching Multimedia Compression). Its main advantage (e.g., in a network application) is its very fast and simple decompression (in a time-domain) that basically consists of reading data without any float-point operations.
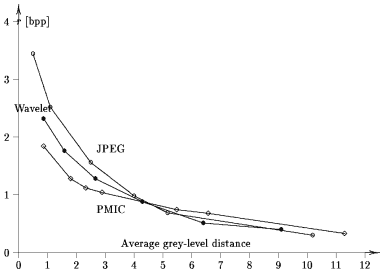
Now, we present in a more detailed fashion the philosophy behind pattern matching approach to multimedia compression. Since nowdays most media are represented in a digital form, it is natural to apply a technique that was proved successful for inherently digital media such as text, namely Lempel-Ziv type schemes We extend Lempel-Ziv approach to lossy (approximate) compression. While it is know that the lossless Lempel-Ziv is asymptotically optimal (i.e., its compression ratio is close to the entropy), we have managed to prove recently that a lossy extension of Lempel-Ziv scheme (of low complexity) is suboptimal (cf. T. Luczak and W. Szpankowski " A Suboptimal Lossy Data Compression Based on Approximate Pattern Matching ). Moreover, we have designed a new lossy (and lossless) compression scheme that works in the time domain and avoids expensive transforms. It is competitive with other competing technologies in terms of compression ratios, far superior in terms of decompression time (extremely fast even with weak computational resources), and promises to provide a way of treating uniformly all kinds of multimedia data (whereas current schemes use different technologies for each). Based on our theoretical results (cf. T. Luczak and W. Szpankowski " A Suboptimal Lossy Data Compression Based on Approximate Pattern Matching ) we can predict the performance of lossless and lossy versions of our data compression scheme. We have also implemented a lossy data compression algorithm for images (called Pattern Matching Image Compression, PMIC in short), and we performed quite extensive experiments on different kinds of structured data which confirmed our theory (cf. M. Atallah, Y. Genin and W. Szpankowski, Pattern matching image compression: Algorithmic and empirical results, and D. Arnaud and W. Szpankowski Pattern Matching Image Compression with Prediction Loop: Preliminary Experimental Results ). For images of good quality our compression ratio is competitive to JPEG and wavelet image compression, however, our theoretical results suggest that we still have a room for further improvements.
The central theme of our approach is the notion of approximate repetitiveness. The detection of the approximate repetitiveness is done by approximate pattern matching, whence the name Pattern Matching Compression (PMC) (e.g., Pattern Matching Image Compression (PMIC), Pattern Matching Audio Compression (PMAC), etc.) This repetitiveness may take different forms in different media, and therefore different distortion measures should be considered, as discussed in the sequel:
Lossless Text Compression. It is well recognized that every text contains some repetitiveness, and Lempel-Ziv type schemes explored it quite well. This repetitiveness can be discovered by a simple exact pattern matching algorithm based on suffix trees (cf. (cf. W. Szpankowski, A generalized suffix tree and its (un)expected asymptotic behaviors). It also seems to us that the next generation of lossless compression of, say, graphic text-like data must use an approach that differs from Lempel-Ziv. That is, in human-made images (such as mechanical or VLSI design images) one expects approximate repetitions of geometric objects. When investigating this aspect of compression (i.e., extension of Lempel-Ziv type compression to graphical objects), we expect that some of our work in the area of computational geometry to be helpful.
Lossy Image Compression. In an image there exists approximate repetitiveness of some areas, and this can be discovered by applying an approximate pattern matching with the quadratic distortion function. We (cf. M. Atallah, Y. Genin, D. Arnaud and W. Szpankowski ) have already implemented this scheme as PMIC.
Video Image Compression. In this context the repetitiveness and approximate repetitiveness are not only within a single frame, but also between two successive frames. Approximate pattern matching seems particularly suited - as a non-transform method - to high-frequency (rapid) changes between frames. This is under our current investigation as a joint project with P. Jacquet (INRIA, France) and L. Georgiadis (Thessaloniki, Greece).
Stereometry and Stereoscopic Display. Clearly, there is a lot of repetitiveness between the ``left eye'' image and the ``right eye'' image. Sophisticated and ``expensive'' methods exist to recognize these, but we propose a simple scheme based on approximate pattern matching that can build a 3D image from 2D pair images (during the compression of 2D pair!). P. Jacquet and I are working currently on it.
Speech and Audio Compression. There is no apparent repetitiveness and approximate repetitiveness in speech and especially audio. It turns out, however, that repetitiveness occurs but shifted in phase, so difficult to recognize in the time occurs but shifted in phase, so difficult to recognize in the time domain. In addition, taking into account the masking effect of audio signals, pattern matching lossy speech and audio compression are possible (as we are currently investigating). Here we might have to apply approximate pattern matching to the Fourier transform to eliminate the (shifted) phase effect in the repeated patterns, but the decompression will be done in the time domain. We are currently working on this project ( A. Gramma, K. Park, and W. Szpankowski).
ORIGINAL: JPEG:
FRACTAL: PMIC:
A more comprehensive comparison of the "Baselope" image is shown in the figure below: