On page 85, I stated that Freese had reproduced, in his Plate 64, Paul-Jean Busschop's 5-piece dissection of a regular hexagon to a square. Freese had claimed without proof in his note at the bottom of Plate 64 that there are an unlimited number of such 5-piece dissections, and that no 4-piece dissection of a regular hexagon to a square is possible.
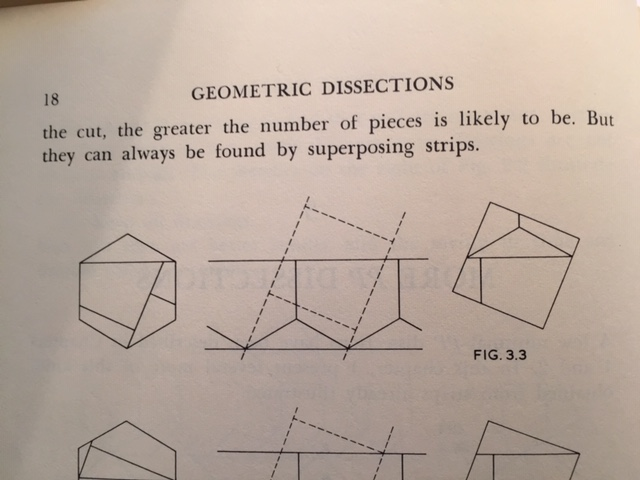
It is true that there are an unlimited number of such 5-piece dissections, but the dissection on Plate 64 does not suggest a proof. We can prove it by using the dissection in Fig. 3.3 on page 18 of Harry Lindgren's book, Geometric Dissections, as we see below. The middle of Fig. 3.3 shows the crossposition of a strip of squares over a strip of hexagon elements. The dissected hexagon on the left in Fig. 3.3 corresponds to the dissected square on the right. Looking at the crossposition in the middle of the figure, suppose that we slide the square upwards within the boundary of the strip of squares, in a northeasterly direction, maintaining the same angle for the strip, and while not changing the topology of the strip crossing. We will get another 5-piece dissection of the hexagon to a square. Indeed, we can achieve an infinite number of different dissections by varying how far we slide the square. It is not clear how we could provide a comparable argument using the dissection in Plate 64.

But we do not know how to prove that no 4-piece dissection of a regular hexagon to a square is possible, using either the dissection in Lindgren's book or Busschop's dissection.
On page 92, I stated that all of the dissections in Plate 76 seemed to be difficult to improve on. Let me amend that assertion to state that we can prove that at least three of the five dissections are minimal.
First, consider the dissection of two regular hexagons to three equilateral triangles at the bottom of the plate. I claim that each of the equilateral triangles must be cut into at least two pieces. Suppose not. Then to avoid having a cut that separates a side of an equilateral triangle into two pieces, that side must be coincident with a diameter of a regular hexagon. But then the equilateral triangle cannot fit entirely within the regular hexagon. Thus each of the equilateral triangles must be cut into at least two pieces.
Second, consider the dissection of six regular hexagons to an equilateral triangle in the upper right corner of the plate. Clearly any dissection that cuts three or more of the hexagons must have at least 9 pieces. When four of the hexagons are not cut, then there is only one way to pack those hexagons into the equilateral triangle without overlap: Each of three hexagons will be pushed as far as possible into a corner, and the fourth hexagon will just fit in the center of the equilateral triangle. But this leaves six separate spaces to be filled in: the three corners of the triangle, plus a space between the middle hexagon and each of the three sides of the triangle. Those six additional pieces will give a total of 10 pieces. Thus a dissection with four uncut hexagons will not be minimal.
Third, consider the dissection of nine regular hexagons to a larger regular hexagon in the upper left corner of the plate. Clearly any dissection that cuts three or more of the hexagons must have at least 12 pieces. When seven of the hexagons are not cut, then there is essentially only one class of ways to pack the seven hexagons: Each of six of the hexagons will be pushed as far as possible into a corner, and the seventh must swim in the interior of the large hexagon. (In the case that not all six corners are filled, then we can always push a hexagon to fill in that corner.) This will force there to be empty space adjacent to each of the middle of the sides of the large hexagon. Each such empty space must be filled separately by an additional piece, thus giving at least 13 pieces altogether. Such a dissection must thus not be minimal.
Copyright 2018, Greg N. Frederickson.
Permission is granted to any purchaser of
Ernest Irving Freese's Geometric Transformations:
the Man, the Manuscript, the Magnificent Dissections!
to print out a copy
of this page for his or her own personal use.
Last updated October 10, 2018.