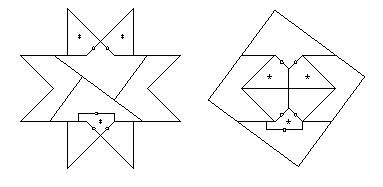This webpage provides further details relating to Table 4.1 on page 45 of
my manuscript Piano-hinged Dissections: Time to Fold!.
The dissections are discussed in the order that they are listed in the table.
This material is all subject to copyright
and may not be reproduced in any form
without the express written consent of the author.
In the discussion below,
DPF refers to
Dissections: Plane & Fancy
HD refers to
Hinged Dissections: Swinging & Twisting and
PhD refers to
Piano-hinged Dissections: Time to Fold!
Also, a dotted line in a figure that contains a twist-hinged dissection
indicates the position of a piano hinge to flip a piece out of the way
in the corresponding piano-hinged dissection.
I show these primarily for each piece that has more than
two twist hinges adjacent to it.
- Pentagon to triangle:
- There is a swing-hinged dissection in HD
Figures 11.31 and 11.32 which uses 8 pieces.
It has one isosceles triangle whose apex connects via a hinge,
which will then
convert to a twist hinge with no additional pieces. The remaining six swing hinges convert to an additional piece plus two additional twist hinges,
producing a 14-piece twist-hinged dissection.
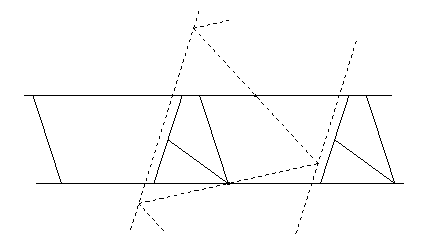
To get the 12-piece twist-hinged dissection that I cite in the table,
use the crossposition above,
which is similar to that in DPF Figure 12.10.
This gives a 6-piece dissection, which we can make swing-
and twist-hingeable by cutting one more piece
and introducing a twist hinge, as I indicate below.
Besides the twist hinge, there are five swing hinges,
each of which converts to an additional piece
plus two additional twist hinges.
This produces the 12-piece
twist-hinged dissection (below) that I cite.
Each piece has at most two adjacent twist hinges.
Thus each needs just one piece to flip away,
giving the 24-piece piano-hinged dissection that I cite.
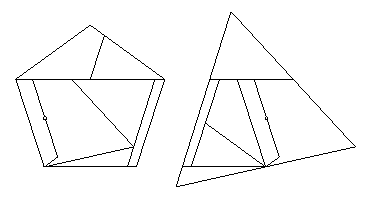
- Pentagon to square:
- The swing-hinged dissection in HD Figures 11.20 and 11.21 is not hinge-snug.
To get the 11-piece twist-hinged dissection that I cite in the table,
I found an unhingeable 7-piece dissection
of a pentagon to a square that is similar in some ways
to Theobald's unhinged dissection of a heptagon to a square.
One of the pieces is a long and very thin right triangle.
The long leg of the triangle has length equal to
the sidelength of the square,
and the length of the short leg of the triangle is
.002789 of the length of the side of the square.
To be able to visualize the process
that produces the twist-hinged dissection,
I show below a dissection of a pentagon
to a rectangle whose length is 1.1559 times its width.
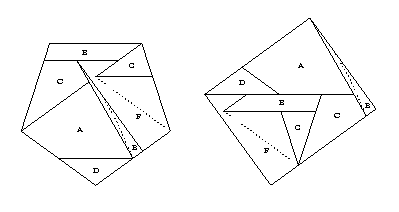
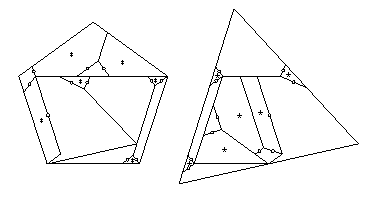
Pieces A and D can readily be swing-hinged together,
as can pieces C and E, and pieces E and F.
Furthermore, there is an isosceles triangle
that we can remove from piece F and combine with piece G
that would allow us to twist the new piece G
and what remains of piece F.
Next, we can carve an isosceles trapezoid out of piece B,
which we can twist-hinge with pieces A, C, and what remains
of piece B.
The isosceles triangle and the isosceles trapezoid are indicated by
dotted lines.
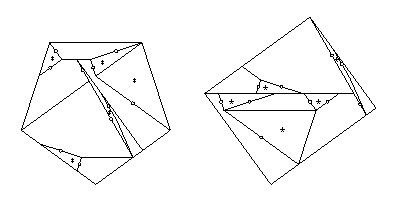
Finally, we convert the three swing hinges, producing
the 11-piece twist-hinged dissection above.
It has one piece
that has three twist hinges adjacent to it,
and each of the remaining ten has at most two adjacent twist hinges.
The one piece needs two pieces
that flip away to expose all three twist hinges.
The other eleven pieces need just one piece to flip away,
giving the 23-piece piano-hinged dissection that I cite.
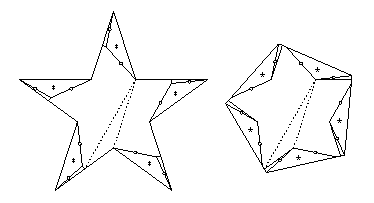
- Pentagram to square:
- There is a 13-piece twist-hinged dissection in HD Figure 22.31.
Ten pieces have at most two twist hinges that are adjacent,
and the remaining three pieces each have three adjacent twist hinges.
The two concave pieces need just one extra piece flipped out of the way,
but the convex piece needs two such additional pieces.
The other ten pieces need just one piece to flip away,
giving the 27-piece piano-hinged dissection that I cite.
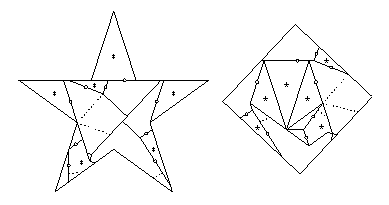
- Pentagram to pentagon:
- There is an 11-piece twist-hinged dissection in HD Figure 22.41.
Ten pieces have at most two twist hinges that are adjacent,
and the remaining piece has five adjacent twist hinges.
The remaining piece needs two additional pieces to flip out of the way.
The other ten pieces need just one piece to flip away,
giving the 23-piece piano-hinged dissection that I cite.
- Hexagon to triangle:
- There is a 7-piece twist-hinged dissection in HD Figure 22.37.
Six pieces have at most two twist hinges that are adjacent,
and the remaining piece has three adjacent twist hinges.
The remaining piece needs two additional pieces to flip out of the way.
The other six pieces need just one piece to flip away,
giving the 15-piece piano-hinged dissection that I cite.
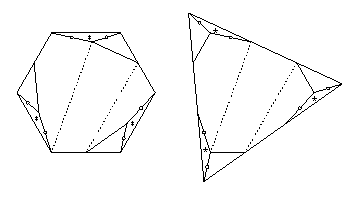
- Hexagon to square:
- The 6-piece swing-hinged dissection
in HD Figures 11.13 and 11.14 is hinge-snug,
which would give us an 11-piece twist-hinged dissection.
However, Gavin Theobald created a 5-piece dissection below
which we can convert into a 6-piece twist-hinged dissection.
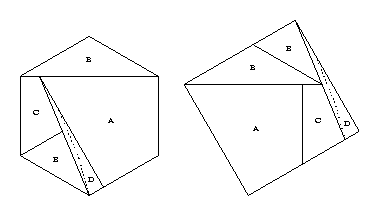
Because piece B is an isosceles triangle,
we can twist-hinge it with pieces A and C.
Furthermore, we can cut an isosceles trapezoid out of piece D,
and twist-hinge this piece with both pieces C and E.
Finally, we can then twist-hinge the isosceles trapezoid with what
remains of piece D,
producing the 6-piece twist-hinged dissection above.
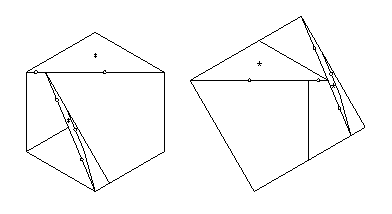
The above dissection has one piece
that has three twist hinges adjacent to it,
and each of the remaining five pieces has at most two adjacent twist hinges.
The one piece needs two pieces
that flip away to expose all three twist hinges.
The other five pieces need just one piece to flip away,
giving the 13-piece piano-hinged dissection that I cite.
- Hexagon to pentagon:
- There is a swing-hinged dissection in HD Solution 11.2 which uses 10 pieces and is hinge-snug.
However, we can do better if we use the crossposition
from Appendix D of Harry Lindgren's book,
as redrawn here:
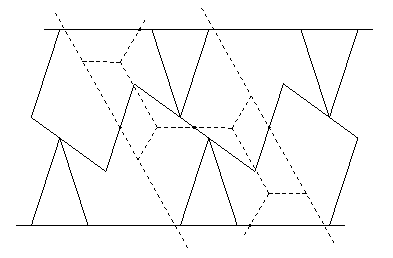
We thus get the 7-piece dissection (solid lines) below.
We then need to hinge piece G (from the pentagon)
onto the rest of the pieces.
We do this as follows:
We split an isosceles trapezoid from piece F,
and place a twist hinge between the trapezoid and what
remains of piece F.
If piece G is swing-hinged to the trapezoid,
then we are able to bring piece G from its position in the pentagon
to the appropriate position in the hexagon.
Noting that pieces A and B form an isosceles trapezoid
in the hexagon,
we flip these pieces over in the hexagon
and connect piece B to piece C with a twist hinge.
There are five swing hinges,
between pieces A and B, C and D, C and E, E and F, and G and the trapezoid.
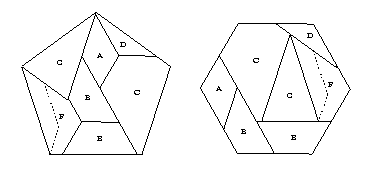
Each of the five swing hinges converts
to an additional piece plus two additional twist hinges,
producing a 13-piece
twist-hinged dissection (below) that I cite.
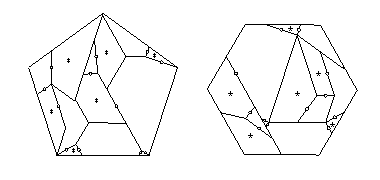
Twelve of the 13 pieces have at most two adjacent twist hinges.
The other piece needs just one piece to flip away,
giving the 27-piece piano-hinged dissection that I cite.
- Hexagon to pentagram:
- Applying the same sort of conversion to HD Figure 21.21
that was applied to HD Figure 21.17 to get HD Figure 22.31,
we get a 15-piece twist-hinged dissection.
Eleven pieces have at most two twist hinges that are adjacent,
three pieces each have three adjacent twist hinges,
and one piece has four adjacent twist hinges.
The three pieces need just one extra piece flipped out of the way,
but the one piece needs two such additional pieces.
The other eleven pieces need just one piece to flip away,
giving the 31-piece piano-hinged dissection that I cite.
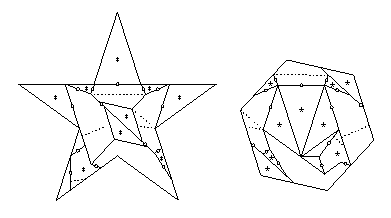
- Hexagram to square:
- There is a 13-piece twist-hinged dissection in HD Figure 22.33.
Eleven pieces have at most two twist hinges that are adjacent,
one piece has three adjacent twist hinges, and one has four.
Those latter two pieces need two pieces each to flip out of the way.
The other eleven pieces need just one piece to flip away,
giving the 28-piece piano-hinged dissection that I cite.
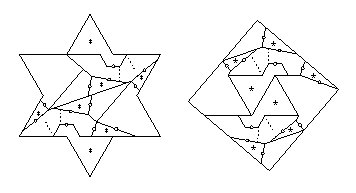
- Hexagram to hexagon:
- There is a 9-piece twist-hinged dissection
at this website.
Eight of the nine pieces are cyclicly hinged.
The only piece that is adjacent to more than two twist hinges
is on the cycle. Thus if we delete one of the two twist hinges
that completes the cycle, we not only remove the redundant hinge
but also ensure that no piece is adjacent to more than two twist hinges.
Then every piece will have one piece that flips away from it,
giving the 18-piece piano-hinged dissection that I cite.
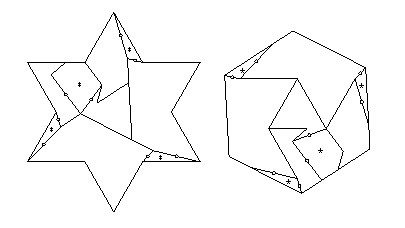
- Heptagon to triangle:
- There is an unhingeable dissection (due to Gavin Theobald)
which is based on a crossposition very similar to the one below.
The resulting 8-piece dissection is in solid lines the following figure.
Note that piece F is an equilateral triangle
of one quarter the area of the given equilateral triangle.
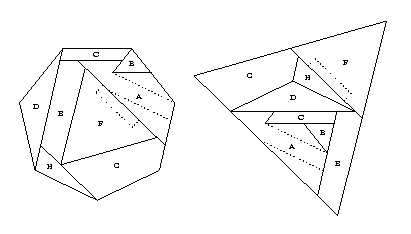
We can convert this dissection
to a 15-piece twist-hinged dissection.
First, enlarge the small isosceles triangle (piece B) by annexing
an isosceles triangle from piece A.
Next, convert the swing hinge between pieces A and C
and then convert the swing hinge between pieces C and E.
As we have seen previously, a byproduct of the latter conversion is that
we can twist-hinge piece D with the little
right triangle created by that conversion.
Then convert the two swing hinges between piece F
and pieces E and G.
To handle piece H in the heptagon,
we swing-hinge it to piece E
and then convert the swing hinge.
To make room for this piece in the full-size equilateral triangle,
we cut an obtuse triangle out of piece A.
Finally, we use a rectangular piece to twist-hinge
the new obtuse triangle onto piece F.
Thus the new obtuse triangle takes the original
place of piece H in the equilateral triangle.
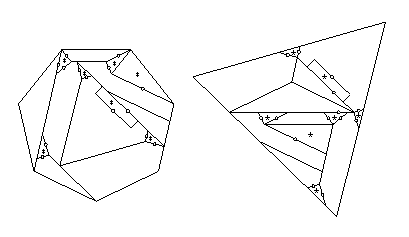
Twelve pieces have at most two twist hinges that are adjacent,
and the remaining three pieces each have three adjacent twist hinges.
Of those, piece F needs only one extra piece flipped out of the way,
if way make the altitude of the rectangle sufficiently small.
Each of the two remaining pieces needs two extra pieces flipped out of the way,
and the other twelve pieces need just one piece to flip away,
giving the 32-piece piano-hinged dissection that I cite.
- Heptagon to square:
- There is an unhingeable dissection (due to Gavin Theobald)
in DPF Figure 11.30 which uses 7 pieces:
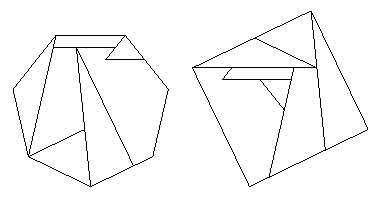
Amazingly, we can convert this dissection
to a 10-piece twist-hinged dissection.
First, enlarge the small isosceles triangle by annexing
an isosceles triangle from an adjacent piece.
Next, convert the swing hinge between the thin trapezoid
and the irregular 7-sided piece.
Then convert the swing hinge between the thin trapezoid
and the irregular quadrilateral.
A remarkable byproduct of this latter conversion is that
we can twist-hinge the large isosceles triangle with the little
right triangle created by the conversion.
Finally, we can twist-hinge the large right triangle
with the two pieces adjacent to it on its left.
These two pieces get interchanged by the new piece
that we carve out of the large right triangle.
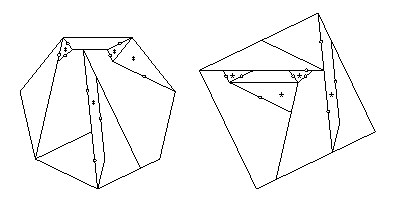
Eight pieces have at most two twist hinges that are adjacent,
and the remaining two pieces each have three adjacent twist hinges.
Each of the two remaining pieces needs two extra pieces flipped out of the way,
and the other eight pieces need just one piece to flip away,
giving the 22-piece piano-hinged dissection that I cite.
- Heptagon to hexagon:
- Gavin Theobald gave an 8-piece unhingeable dissection
of a regular heptagon to a hexagon.
To be able to produce a twist-hinged dissection,
we shall use his heptagon strip
with a different hexagon strip
in the crossposition below,
followed by the resulting 9-piece partially-hinged dissection (solid lines):
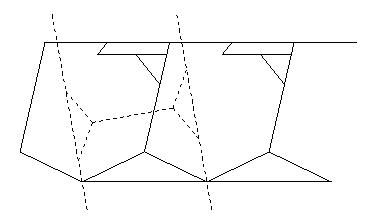
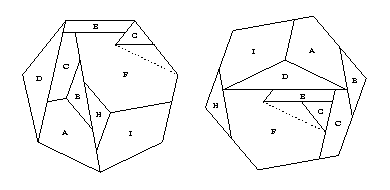
We can convert this dissection
to a 15-piece twist-hinged dissection.
First, enlarge the small isosceles triangle (piece G) by annexing
an isosceles triangle from piece F.
Next, convert the swing hinge between pieces E and F
and then convert the swing hinge between pieces C and E.
Again, a byproduct of the latter conversion is that
we can twist-hinge piece D with the little
right triangle created by that conversion.
Finally, convert the four remaining swing hinges,
between pieces A and B, B and C, F and H, and H and I.

Fourteen pieces have at most two twist hinges that are adjacent,
and the remaining piece has three adjacent twist hinges.
That piece needs two extra pieces flipped out of the way,
and the other fourteen pieces need just one piece to flip away,
giving the 31-piece piano-hinged dissection that I cite.
- {7/2} to heptagon:
- There is a 15-piece twist-hinged dissection in HD Figure 22.43.
Fourteen pieces have at most two twist hinges that are adjacent,
and the remaining piece has seven adjacent twist hinges.
The one piece needs two extra pieces flipped out of the way,
and the other fourteen pieces need just one piece to flip away,
giving the 31-piece piano-hinged dissection that I cite.
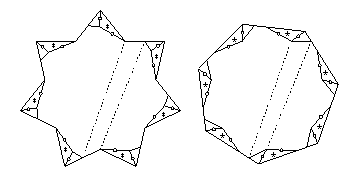
- Octagon to triangle:
- There is a 12-piece twist-hinged dissection
at this website.
Eleven pieces have at most two twist hinges that are adjacent,
and the remaining piece is adjacent to three twist hinges.
We can flip just one piece away from this one, if we hinge
the new piece at the corner farthest from the twist hinges.
Every other piece will have one piece that flips away from it,
giving the 24-piece piano-hinged dissection that I cite.
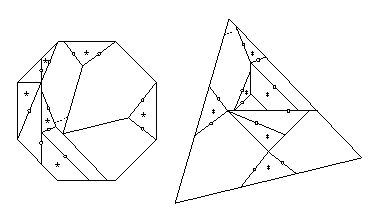
- Octagon to square:
- There is a 9-piece twist-hinged dissection in HD Figure 22.40.
Eight pieces have at most two twist hinges that are adjacent,
and the remaining piece has four adjacent twist hinges.
The one piece needs two extra pieces flipped out of the way,
and the other eight pieces need just one piece to flip away,
giving the 19-piece piano-hinged dissection that I cite.
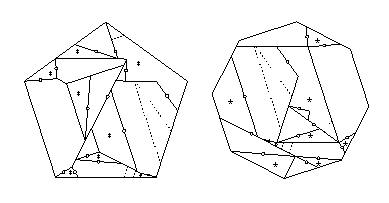
- Octagon to pentagon:
- There is a 16-piece twist-hinged dissection
at this website.
Thirteen pieces have at most two twist hinges that are adjacent,
and the remaining three pieces are each adjacent to three twist hinges.
We can flip just one piece away from one of these, if we hinge
the new piece at the corner farthest from the twist hinges.
For the other two, we must flip away two pieces each.
Every other piece will have one piece that flips away from it,
giving the 34-piece piano-hinged dissection that I cite.
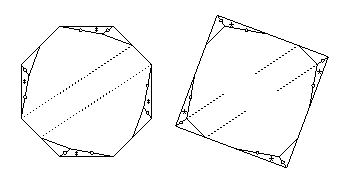
- {8/2} to square:
- The 8-piece swing- and twist-hinged dissection
in HD Figures 21.9 and 21.10
is hinge-snug, giving us the 11-piece twist-hinged dissection
that I cite in the table.
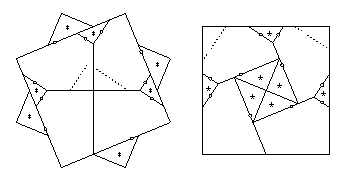
The twist-hinged dissection has two pieces that each have three twist hinges
adjacent to them, and each of the remaining nine pieces has at most two adjacent twist hinges.
The two pieces each need just one piece to flip away,
since two of the sides that have twist hinges are parallel.
The piano hinge to flip away such a piece
is then perpendicular to those sides.
The other ten pieces need just one piece to flip away,
giving the 22-piece piano-hinged dissection that I cite.
- {8/3} to square:
- There is an 8-piece strip dissection of an {8/3} to a square.
We form the strip for the {8/3} by cutting off four of its points
and nestling them between the other four.
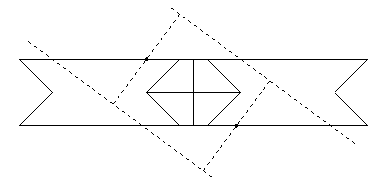
- If we position the square strip appropriately,
then we can steal a bit of area from the four cut-off points
and twist-hinge what remains of them onto
the neighboring piece in the {8/3}.
Actually, we can't position the square strip to handle
all four points simultaneously, and we need one more piece
(with three twist hinges) to effect the appropriate shift.
We get a 9-piece swing- and twist-hinged dissection
that is still hinge-snug (below) with three swing hinges
and five twist hinges.
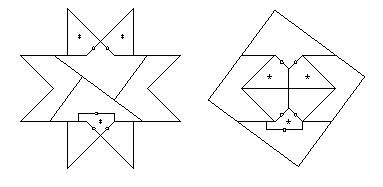
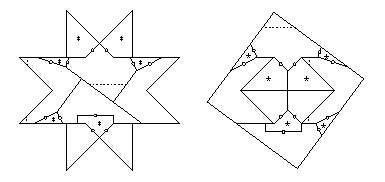
Performing the conversion on this,
we get a 12-piece twist-hinged dissection (below).
Ten pieces have at most two twist hinges that are adjacent,
one piece has three adjacent twist hinges,
and one piece has four adjacent twist hinges.
The latter piece needs just one piece flipped away, as shown,
and I also show that a concave piece with two adjacent hinges
needs just one piece flipped away.
The only piece that needs two pieces flipped away is the one
with three adjacent twist hinges.
Thus we get the 25-piece piano-hinged dissection that I cite.
- {8/3} to hexagon:
- There is a 10-piece strip dissection of an {8/3} to a hexagon.
We use the same strip for the {8/3} as we did in the preceding dissection.
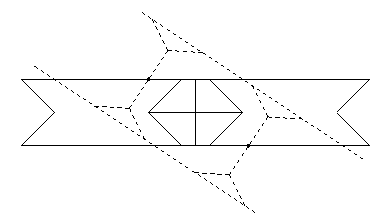
- If we position the hexagon strip appropriately,
then we can steal a bit of area from the four cut-off points
and twist-hinge what remains of them onto
the neighboring piece in the {8/3}.
As in the last dissection, we can't position the hexagon strip to handle
all four points simultaneously, and we need one more piece
(with three twist hinges) to effect the appropriate shift.
We get an 11-piece swing- and twist-hinged dissection
that is still hinge-snug (below) with three swing hinges
and seven twist hinges.
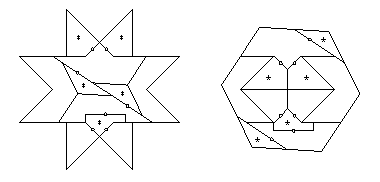
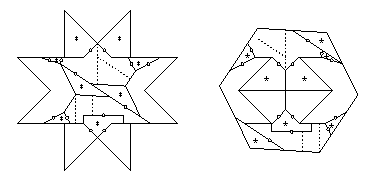
Performing the conversion on this,
we get a 14-piece twist-hinged dissection (below).
Eleven pieces have at most two twist hinges that are adjacent,
two pieces have three adjacent twist hinges,
and one piece has five adjacent twist hinges.
Each of the last three pieces needs just two pieces flipped away,
and I have shown this for two of the three.
Each of the remaining eleven pieces
needs just one piece flipped away.
Thus we get the 31-piece piano-hinged dissection that I cite.
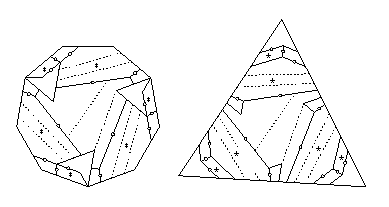
- Enneagon to triangle:
- There is a 16-piece twist-hinged dissection in PhD Figure 3.14.
Twelve pieces have at most two twist hinges that are adjacent,
and the remaining four pieces each have three adjacent twist hinges.
These four pieces need two extra pieces flipped out of the way.
The other twelve pieces need just one piece to flip away,
giving the 36-piece piano-hinged dissection that I cite.
- Decagon to triangle:
- If we twist around four triangles in a decagon,
then we get a tessellation element for the plane.
From that element, we can produce a strip element
that works well for triangles, giving us
a 10-piece swing- and twist-hinged dissection
that is hinge-snug.
By flipping over two pieces in the decagon,
we get a 10-piece swing- and twist-hinged dissection
that is still hinge-snug (below) that has one fewer swing hinge
and one more twist hinge.
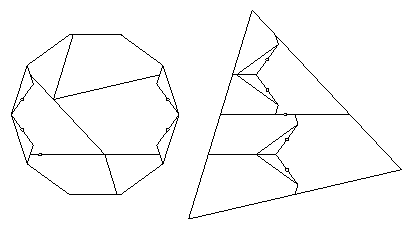
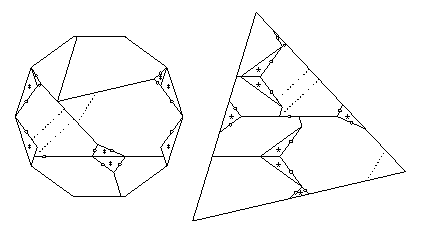
Performing the conversion on this,
we get a 14-piece twist-hinged dissection (below).
Twelve pieces have at most two twist hinges that are adjacent,
one piece has four adjacent twist hinges,
and one piece has five adjacent twist hinges.
The latter piece needs two pieces flipped away.
All other pieces need just one piece to flip away,
giving the 29-piece piano-hinged dissection that I cite.
- Decagon to square:
- We start with the same tessellation as in the
previous dissection, of a decagon to a square.
We then can produce a different strip element
that works well for squares (below).
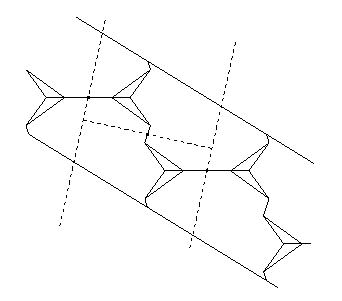
The crossposition gives us
a 10-piece swing- and twist-hinged dissection
that is hinge-snug (below).
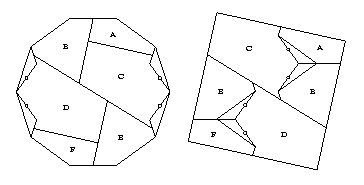
The six pieces A through F
can be connected by swing hinges,
and it is possible to convert each of the five swing hinges
to twist hinges.
This would give a 15-piece twist-hinged dissection.
However, we can do better by cutting a zigzag piece
out of pieces C and D,
and then using this one piece to twist-hinge pieces B through E.
We finish by converting the swing hinge between pieces A and B,
and the swing hinge between pieces E and F.
We thus get the 13-piece twist-hinged dissection (below).
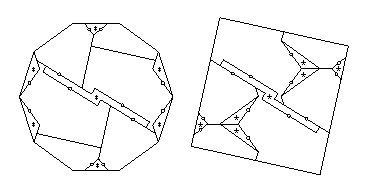
Ten pieces have at most two twist hinges that are adjacent,
two pieces each have three adjacent twist hinges,
and one piece has four adjacent twist hinges.
The latter piece needs two pieces flipped away.
The other twelve pieces need just one piece to flip away,
giving the 27-piece piano-hinged dissection that I cite.
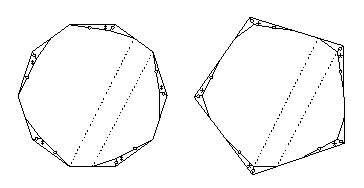
- Decagon to pentagon:
- There is an 11-piece twist-hinged dissection in PhD Figure 3.9.
Ten pieces have at most two twist hinges that are adjacent,
and the remaining piece has five adjacent twist hinges.
The one piece needs two extra pieces flipped out of the way,
and the other twelve pieces need just one piece to flip away,
giving the 23-piece piano-hinged dissection that I cite.
- Dodecagon to hexagon:
- There is a 9-piece twist-hinged dissection
at this website.
Eight of the nine pieces are cyclicly hinged.
The only piece that is adjacent to more than two twist hinges
is on the cycle. Thus if we delete one of the two twist hinges
that completes the cycle, we not only remove the redundant hinge
but also ensure that no piece is adjacent to more than two twist hinges.
Then every piece will have one piece that flips away from it,
giving the 18-piece piano-hinged dissection that I cite.
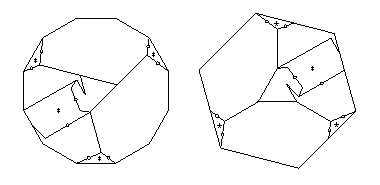
- {12/2} to square:
- The swing-hingeable dissection in
HD Figures 11.53 and 11.54 is not hinge-snug.
However, we can create a strip element from doing
the twists that we see in Figure 21.11,
and then get a 12-piece swing- and twist-hinged dissection (below)
that is hinge-snug.
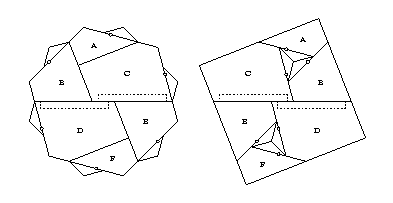
The six pieces A through F
are connected by swing hinges,
and we can convert each of the five swing hinges
to twist hinges.
This would give a 17-piece twist-hinged dissection.
We can do better by cutting a zigzag piece
out of pieces C and D by taking a rectangle from C
and a rectangle from D and combining them.
We use this one piece to twist-hinge pieces B through E
together.
As before, we finish by converting the swing hinge between pieces A and B,
and the swing hinge between pieces E and F.
We thus get a 15-piece twist-hinged dissection below.
Twelve pieces have at most two twist hinges that are adjacent,
two pieces have three adjacent twist hinges,
and one piece has four adjacent twist hinges.
The three pieces each need two extra pieces flipped out of the way.
The other twelve pieces need just one piece to flip away,
giving the 33-piece piano-hinged dissection that I cite.
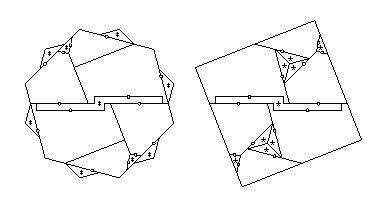
- {12/2} to hexagon:
- The 10-piece swing- and twist-hinged dissection
in HD Figures 21.11 and 21.12 is hinge-snug,
giving us the 13-piece twist-hinged dissection that I cite in the table.
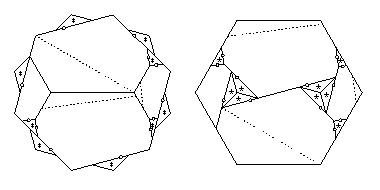
The twist-hinged dissection has two pieces that each have three twist hinges
adjacent to it, and one piece that has four adjacent twist hinges.
Each of the remaining ten pieces has at most two adjacent twist hinges.
The piece with four adjacent twist hinges and the piece with three
twist hinges that is adjacent to it
each need just one piece to flip away,
since two of the sides that have twist hinges are parallel.
The piano hinge to flip away such a piece
is then perpendicular to those sides.
The other piece with three twist hinges needs to flip away just one piece,
as do the other ten pieces,
giving the 26-piece piano-hinged dissection that I cite.
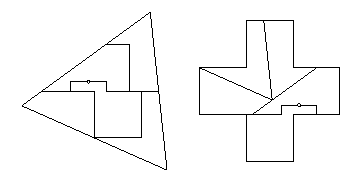
- Greek Cross to triangle:
- The swing-hingeable dissection in
HD Figure 11.40 is not hinge-snug.
However, we can modify Lindgren's 5-piece unhingeable dissection in
DPF Figure 11.40
to get a 5-piece swing- and twist-hinged dissection
that is hinge-snug (below).
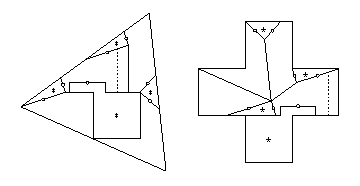
Performing the conversion on this,
we get an 8-piece twist-hinged dissection (below).
Seven pieces have at most two twist hinges that are adjacent,
and the eighth piece has three adjacent twist hinges.
The latter piece needs just one piece flipped away,
with the piano hinge as shown.
The other seven pieces need just one piece to flip away,
giving the 16-piece piano-hinged dissection that I cite.
- Greek Cross to dodecagon:
- We adapt the 9-piece twist-hinged dissection
of a dodecagon to a square in HD Figure 22.30,
drawing inspiration from the swing-hinged dissection
of a dodecagon to a Greek Cross in Solution 10.2.
Specifically, we replace the long segments in Figure 22.29
with the zigzag segments from Solution 10.2 that give the boundary
of the Greek Cross. This results in a 9-piece twist-hinged dissection.
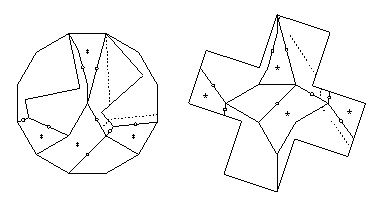
The twist-hinged dissection has one piece that has three twist hinges
adjacent to them,
and each of the remaining eight pieces has at most two adjacent twist hinges.
The one piece needs two pieces that flip away,
one to expose the twist hinge to its neighboring quadrilateral,
and the other to expose the other two twist hinges.
I also show the piano hinge for the other neighbor
of the neighboring quadrilateral.
This gives the 19-piece piano-hinged dissection that I cite.
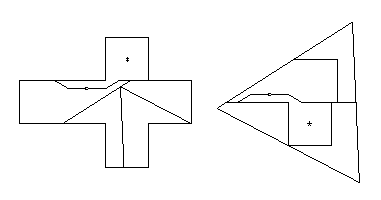
- Latin Cross to triangle:
- The swing- and flip-hingeable dissection in
HD Figure 21.13 is not hinge-snug.
However, we can change the pieces connected by the flip hinge
so that they are connected by a twist hinge
and at the same time open up space to which we attach a swing hinge
that is hinge-snug.
We then get a 5-piece swing- and twist-hinged dissection
that is hinge-snug (below).
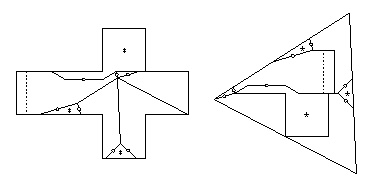
Performing the conversion on this,
we get an 8-piece twist-hinged dissection (below).
Seven pieces have at most two twist hinges that are adjacent,
and the eighth piece has three adjacent twist hinges.
The latter piece needs just one piece flipped away,
with the piano hinge as shown.
The other seven pieces need just one piece to flip away,
giving the 16-piece piano-hinged dissection that I cite.
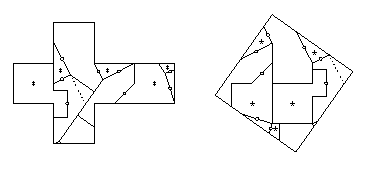
- Latin Cross to square:
- There is an 11-piece twist-hinged dissection in HD Figure 22.36.
Ten pieces have at most two twist hinges that are adjacent,
and the remaining piece has three adjacent twist hinges.
The one piece needs only one extra piece flipped out of the way,
if we place the new piano hinge toward the longest leg of the cross.
The other ten pieces need just one piece to flip away,
giving the 22-piece piano-hinged dissection that I cite.
Last updated May 1, 2006.