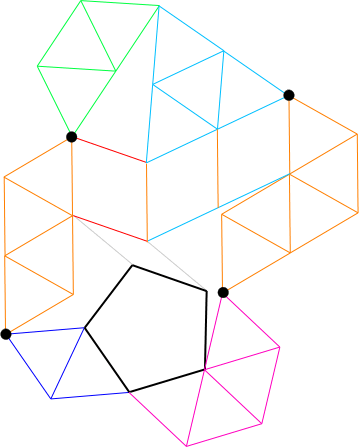
- First, Gavin used the same basic idea as O'Beirne to produce an angle of 180 degrees.
At the top of the figure, he used the rigid group of 7 green rods, the rigid group of the top 9 of the light blue rods,
and the highest red rod to construct an isosceles triangle with side lengths of 1, 2, and 2.
As I demonstrated in Figure T7 on page 71, that isosceles triangle when appended with an equilateral triangle
of side length 1, gives a kite-like figure whose long diagonal is sqrt(3)(1+sqrt(5))/2.
But Gavin produced this length between the top two black dots:
From the upper right dot, he has a straight length of 2 (along 2 light blue rods)
followed by the red rod at the base of the isosceles triangle.
He has the appropriate angle between the 2 light blue rods and the red rod,
because that is the same angle as in the kite-like figure in Figure T7.
- Next, Gavin forced the four black dots to be the vertices of a parallelogram as follows.
He used a rigid group of 9 orange rods on the left to force the leftmost two black dots to be at distance sqrt(7).
He used a rigid group of 11 orange rods on the right to force the rightmost two black dots to be at distance sqrt(7).
He linked these two groups together by a sequence of three rhombuses connected by the remaining orange rods.
These rhombuses force the two orange rods in the middle, plus the two on either side, to be parallel.
That forces the two line segments, one between the black dots on the left and the other between the black dots on the right,
to be parallel.
- Once there is a parallelogram, we can conclude that opposite sides are the same length,
and thus the distance between the bottom two black dots is also sqrt(3)(1+sqrt(5))/2.
Gavin formed a triangle using this length as a base,
by using the rigid group of four dark blue rods plus the lower left black rod to get a length of sqrt(3),
and by using the rigid group of eight violet rods plus the lower right black rod to get a second length of sqrt(3).
As discussed on page 71, such a triangle has an angle of 108 degrees.
It follows that the lowest angle in the pentagon (call it the apex) is 108 degrees.
(The sides of the angle are rotated 30 degrees from with respect to the sides of length sqrt(3).)
- Finally, Gavin's construction forces the side of the pentagon that is opposite to the apex (let's call that side the base) to be at the correct angle to make the pentagon be regular: First, the two grey rods help form a rhombus, so that the pentagon's base is parallel to the base (upper red rod) of the isosceles triangle with sides of 1, 2, and 2. That red rod is at an angle of 30 degrees with the line segment joining the top two black dots. That follows because the kite can overlay with endpoints as the top two black dots, with the equilateral triangle on the left, and thus bisected by the line segment. Then the pentagon's base is at an angle of 30 degrees with a line segment between the bottom two black dots. The pair of pentagon edges at the apex are rotated 30 degrees from the two line segments of length sqrt(3), which means that a diagonal through the two vertices of the pentagon between the apex and the base will be parallel to the base. Thus the base is indeed at the correct angle.
"Bracing regular polygons as we race into the future,"The article was also selected for inclusion in:
College Mathematics Journal, Vol. 43, No. 1, pp. 43-49, 2012.
Martin Gardner in the Twenty-First Century, ed. Michael Henle and Brian Hopkins, Mathematical Association of America, Washington, DC (2012), pp. 11-18.(Note that my middle initial is erroneously identified as "W" in that book.)
Andrei Khodulyov's bracings
In an update to Math Magic, Erich Friedman reported better results for bracing regular polygons when the rods are allowed to cross each other. Erich learned from Serhiy Grabarchuk that Andrei Khodulyov had found the following: bracing a square with 15 additional rods, a pentagon with 26 rods, a heptagon with 72 rods, an octagon with 23 rods, an enneagon with 42 rods, a decagon with 45 rods, a hendecagon with 144 rods, a dodecagon with 37 rods.
Gerard 't Hooft's Meccano Math
A related, yet interesting, topic is how to take strips containing holes at fixed integral distances apart and bolt them together to make planar figures such as regular polygons. Physicist (and Nobel Prize winner) Gerard 't Hooft has written a paper, "Meccano Math", about such constructions. Meccano is the tradename for sets of such strips and connectors that have been produced for children for some number of years. (In the United States, such sets were produced under the name of Erector Sets.) 't Hooft develops a theory that allows him form rational numbers and takes square roots, form straight lines, and bisect angles. He gives several constructions that form regular pentagons, one with as few as seven strips, a construction that forms a regular heptagon using only 15 strips, and a general construction that creates a regular n-gon out of 10n-27 strips, whenever n is odd.
Copyright 2001-2012, Greg N. Frederickson.
Permission is granted to any purchaser of
Hinged Dissections: Swinging & Twisting
to print out a copy
of this page for his or her own personal use.
Last updated January 19, 2015.