Hinged models for area and volume formulas - wonderful examples for
Hinged Dissections: Swinging & Twisting, by Greg N. Frederickson:

When I visited Butler University on Columbus Day of 2003, Jerry Farrell showed me several handsome wooden models that he thought had been the property of the mathematician and astronomer Harry E. Crull (1909-1972). Jerry rescued the models shortly before they were to be discarded. (!) They had been sitting in a storage cabinet since 1965.

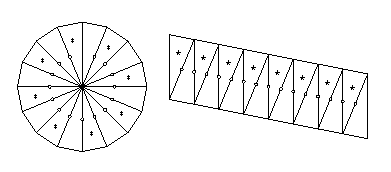
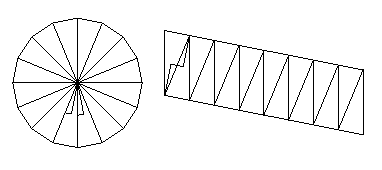
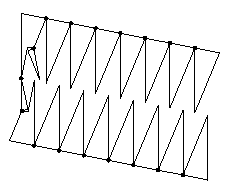
The first model consists of two swing-hinged assemblages of isosceles triangles that together approximate the dissection of a circle into a (radius x (pi * radius))-rectangle, and leads in the limit to the well-known formula for the circle's area: Area = pi * radius * radius. The hinging was accomplished by means of a cloth tape that was tacked onto the wood.

Everyone should remember the above formula from geometry, especially Long John Silver! (Note the following cartoon by Pat Byrnes from The New Yorker, March 16, 2017:)

In 2004 I found out that a model like Crull's was described in US patent 137075, "Improvement in apparatus for teaching mensuration," by Isaac Harrington, March 25, 1873. Excerpting from the patent:
"Fig. 3 is a plan view of a block for demonstrating and proving the rule for the measurement of regular polygons, by means of which it can be readily shown that by multiplying one-half of the diameter by one-half of the circumference the product will represent the superficial area. The said block is divided into as many triangular sections d as the figure has sides, which said sections d d d are hinged together at the periphery of the figure so that they may be transposed and arranged in the position shown in Fig. 3a. The drawing shows a dodecagon; but any polygon having four or more equal sides may be represented in the same manner; and I may also state that the area of a circle may be calculated in the same manner, very nearly, by supposing the circumference to be composed of an infinite number of right lines."

     

     

If you prefer a single assemblage rather than two, then it is easy to switch to a twist-hinged model, which I identify in the diagram below. The small circles represent the twist hinges (see chapter 22 of Hinged Dissections), and the asterisks and small stars indicate the pieces that are flipped an odd number of times. This is reminiscent of, but simpler than, a new family of twist-hinged dissections that I have found. Also, check out a similar, though unhinged, instructional aid for the area of a circle that is currently being supplied by AplusCompass.com.

But what about getting a swing-hinged model that has just one assemblage? This is possible too, if we use two more pieces: a pair of right triangles. The right triangles nestle into cavities in the two concave pieces. In going from the regular polygon to the parallelogram, these right triangles switch which concave piece they nestle with.

The second model consists of two swing-hinged assemblages of isosceles-triangular prisms that together approximate the dissection of a cylinder into a (radius x (pi * radius) x height)-rectangular solid, and leads in the limit to the well-known formula for the cylinder's volume: Volume = pi * radius * radius * height. That's a rubber band that I used to try to pull the two assemblages around to form the cylinder.

     

     



The third model consists of one swing-hinged assemblage of pieces that together approximate a cone sitting on top of a cylinder of the same radius. When I originally saw this model, it was not clear what the ultimate purpose was. After seeing the following model, I believe that this one and the next one are not dissections of one figure to another, but only derivations of formulas for volume. This model uses 12 pieces, each a pyramid atop a small triangular base, to approximate a cone. (We should ignore the base on each piece, which had been placed there to allow the pieces to be hinged together.) The volume of each pyramid is (1/3)*(area of the base)*height. As the number of pieces is allowed to increase, the total area of all of the bases will approach the area of a circle, which is pi*radius*radius. Thus, in the limit, the volume of the cone will be (1/3)*pi*radius*radius*height.

     

I received a fourth model from Jerry a couple of weeks after the others. It consists of 32 pieces that hinge together to form a ball. (The first photo shows the ball from the top, with string wrapped around eight tacks to hold it together, and the second photo shows the ball from the bottom, with a round piece of leather serving as a multiple hinge to eight of the pieces.) It seems clear that this model is a visual demonstration of an approximation of the volume of a sphere: Each of the 32 pieces approximates a pyramid, whose volume is (1/3)*(area of the base)*height. The sum of areas of all of the surfaces that would correspond to the bases will be the area of the surface of the ball, which is 4*pi*radius*radius. If we cut the ball into more and more pieces, they will become closer and closer to true pyramids, whose height will be the radius of the ball. In the limit, we get an exact value for the volume of the ball: (4/3)*pi*radius*radius*radius.

     

Tracking down the origin of these models

In an attempt to pin down the origin of the models, I located Harry Crull's son, Harry E. Crull, Jr., and asked him about the models. He didn't recall seeing them, even though he was a math major at Butler and his father's primary assistant at the Holcomb Observatory and Planetarium. Yet Jerry Farrell pointed out that Dr. Crull was the geometer and had introduced many courses (perhaps a dozen in all) at Butler. Jerry suggested that perhaps the models were made by students or in Butler's woodshop. He noted that no other faculty members since Crull's time have been geometers.

In 2005, Dr. Peggy Kidwell, Curator of Mathematics at the Smithsonian Institution, observed that these models are very close to some produced by Albert H. Kennedy (1848-1940) of Rockport, Indiana.

In July 2006, I received the following email message from George Huffman:
With reference to the wooden geometry models that you have illustrated on the web page, I can indeed confirm that they were the creation of "Prof." Kennedy of Rockport, Indiana. He apparently created these as instructional tools for high school teachers in the 1920s. I have a complete set (exactly like those illustrated) plus an instruction book that accompanied them. I believe that you have the complete set also.
My father, Millard Huffman, lived with the Kennedy family (relatives of my family) when he went to high school in Rockport in the late 1920s. "Prof." Kennedy (as he was called) was an extremely well educated man with an extensive science background. He had a major influence upon my father who in turn passed on this love of science to me and my brothers.
My cousin has another set of models created by Prof. Kennedy, and I know that the public library in Rockport has yet another set; I have encountered another set on eBay some years ago. If you would like a copy of the instruction book send me your address and I will try to dig it up and make a copy.
The instruction book, The Arithmetic of Practical Measurements: A Manual for the use of Teachers accompanying A. H. Kennedy's Dissected Blocks, published by A. H. Kennedy in Rockport, Indiana, contains 13 pages of text that gives hints on how to present various geometric figures and the formulas for area and volume as well as practical exercises. It has sections on the rectangle, the parallelogram, the triangle, the trapezoid, the circle, the rectangular solid, the pyramid, the cylinder, the cone, the globe, square root, and cube root. Additional models are mentioned in the book, but when I queried George Huffman further, he replied:
My set of demonstration blocks is exactly like the ones that you pictured. I'm pretty sure that my cousin has the same set and the public library in Rockport has this set minus one. I have never seen the cube, square root blocks, etc. if they exist.
Kennedy became superintendent of the Rockport schools in 1878. (See History of Warrick, Spencer and Perry Counties, Indiana: from the earliest time to the present; together with interesting biographical sketches, reminiscences, notes, etc., Chicago, Goodspeed, 1885.)

Acknowledgments:

Thank you, Jerry, for showing me these models and allowing me to post photographs of them on the web.

In December 2004, Jerry and I discussed the possibility of his donating the four models to the Smithsonian. After he and his wife Karen visited the museum in February 2005, Jerry decided to donate the models, and sent the last of them in early March. Through his generosity, future generations will be able to enjoy our mathematical cultural heritage.

Thank you, Peggy, for identifying what ended up being the true origin of the models.

Thank you, George, for sharing your history of the models, as well as sending a copy of the instruction book.


January 2011: Check the webpage Albert H. Kennedy's mensuration blocks for recent developments regarding Kennedy's blocks!

Back to the photo gallery for Hinged Dissections: Swinging & Twisting.

June 2015: To get a 21st century view of a model for the area of a circle, see Edward Ball's Area of a circle (Rearrangement Method).


Copyright 2003-2019, Greg N. Frederickson.
Permission is granted to any purchaser of Hinged Dissections: Swinging & Twisting to print out a copy of this page for his or her own personal use.

Last updated July 22, 2019.