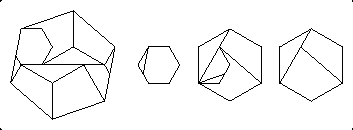
A couple months before the book appeared, I wondered if there was a nice hinged dissection of hexagons for 12 + (sqrt(3))2 + (sqrt(3))2 = (sqrt(7))2. Indeed, I found that there is a 10-piece hinged dissection. One can cut a sqrt(3)-hexagon into three pieces that give give two sides of the sqrt(7)-hexagon. Doing this twice leaves empty spots on opposite ends of the sqrt(7)-hexagon. Since we can have just three hinged assemblages, we need a further trick, to fill up one of the empty spots. Given the hingeable dissection below, do you see how to hinge the pieces? There's more than one way to do it.
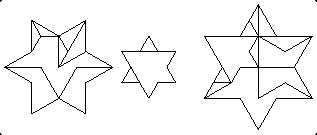
My first book shows a 9-piece dissection by Robert Reid of hexagrams for 12 + (sqrt(3))2 = 22 which had bettered my own 10-piece dissection. Now Robert has done it to me again, improving my 12-piece hinged dissection to an 11-piece dissection.
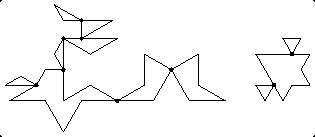
Robert's dissection is wobbly hinged, but it can be converted to a 12-piece hinged dissection that isn't wobbly. Just make one cut in the 10-sided piece. Do you see how?
Copyright 2002, Greg N. Frederickson.
Permission is granted to any purchaser of
Hinged Dissections: Swinging & Twisting
to print out a copy
of this page for his or her own personal use.
Last updated May 14, 2002.