Updates to Chapter 3, "Tricks for Turning",
in Hinged Dissections: Swinging & Twisting, by Greg N. Frederickson

• A better explanation for the Q-slide (Q-swing)

A better explanation for the Q-slide (Q-swing)

Roberto Doniez found my description of a Q-slide difficult to follow, and when I looked at it after 17 years, so did I! I had neglected to state that two edges in Figure 3.11 need to be the same length, and also did not give an easy way to generate the dissection. So here is a description that is hopefully easier to follow:

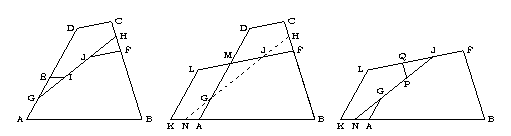
Consider the middle of the figure, which contains quadrilaterals ABCD and BFLK, which we would propose to dissect one into the other.
Note that the quadrilaterals are positioned so that the points B overlap in each, as do points A and points F.
Place point H on edge BC halfway between points C and F. Place point N on edge BK halfway between points A and K. Draw edge HN between points H and N.
Let J be the point at which edges HN and FL intersect. Let G be the point at which edges HN and AD intersect.
Place point E on edge AD so that E is at twice the distance from A that G is.
Place point I on edge GH so that edge EI is parallel to edge AB.
Place point Q on edge FL so that Q is at twice the distance from F that J is.
Place point P on edge JN so that edge PQ is parallel to edge FB.
Finally, draw the edges as on the left and right in the figure below.

Copyright 2014-2014, Greg N. Frederickson.
Permission is granted to any purchaser of Hinged Dissections: Swinging & Twisting to print out a copy of this page for his or her own personal use.

Last updated June 4, 2014.