During the summer and fall of 2005, I derived a wide variety of twist-hinged dissections, using some nifty techniques. These dissections are presented in two papers,
- "Unexpected Twists in Geometric Dissections", Graphs and Combinatorics, 23[Suppl] (2007), pp. 245-258, and
- "The Heptagon to the Square, and Other Wild Twists", Mathematical Intelligencer, Vol. 29, No. 4, pp. 23-33, 2007.
There is a cute twist-hinged dissection proof that a2 – b2 = (a+b)(a–b). It uses only two pieces (just like the ellipse-to-heart dissection), or three, if you have a piece for the b-square. It is so easy that I won't put the solution here. The proof (without twist hinges) is given in "Veranshaulichung von a2 – b2 = (a + b) (a – b)", by Franz Denk, Unterrichtsblätter für Mathematik und Naturwissenschaften, volume 44 (1938) page 23. At the time, Denk was at Erlangen. Later, he was a professor at the University of Regensburg and one of three editors of Archimedes, a German periodical (published 1949-72) with suggestions and exercises for teachers, pupils, and friends of mathematics. Denk was born in 1897 in Ingolstadt. Starting in 1922, he was an instructor for math and physics, and during the second world war was a meteorologist.
Converting Robert Reid's hinge-snug dissection of hexagons for 12 + 22 + 22 = 32 in Figure 8.7 gives an 11-piece twist-hinged dissection. However, I have found a nifty 8-piece twist-hinged dissection.

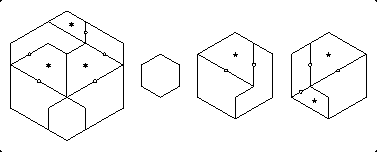
On pages 243-244, I had derived a 13-piece twist-hinged dissection of a hexagram to a square. In November 2006 I found the 12-piece dissection shown below. I convert two swing hinges, use four applications of hinge-reflectiveness, and use the P-twist. As a bonus, the dissection is rotationally symmetric.
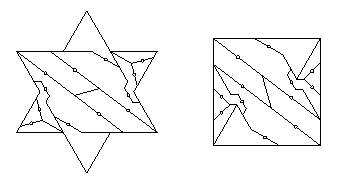
On pages 244-245, I had derived an 11-piece twist-hinged dissection of a Latin Cross to a square. Gavin Theobald sent me a message in December 2008, identifying an improvement:"The dissection of figure 22.35 can also be improved by one piece. This is one I found years ago, but I don't think I ever got round to telling you about it. A strip element can be formed out of just two pieces instead of the three of figure 22.34. In figure 22.34, remove the right hand square and reattach it at the left. The rest should be obvious. Of course this solution is now superseded by the improvement given on your web pages, but I thought you would like to know of the improvement anyway."In the meantime (in March 2007) I found and posted the 7-piece dissection shown below. This was somewhat of a joint effort with Gavin. He had come up with a new unhinged dissection of a Latin Cross to a square based on completing the tessellation. His dissection didn't reduce the number of pieces for an unhinged dissection. But when I looked at the dissection, I realized that it was convertible to a 7-piece twist-hinged dissection. After I informed him of this, he said he had been thinking along the same lines. Note that I left the star and the asterisk off of the thinnest piece, because there isn't room, but clearly, that piece must be turned over.
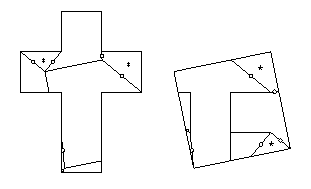
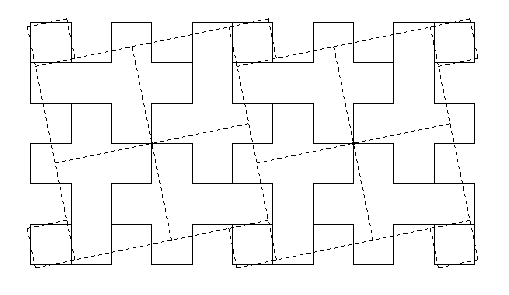
Below is the superposition of the tessellations. For each set of four Latin crosses, there is a small square, and similarly for each set of four large squares. We see the tessellation of Latin crosses and small squares in solid lines, and the tessellation of large squares and small squares in dashed lines. The dashed edges cut each cross into five pieces which form the square when one of the pieces gets turned over. Note that the small squares share their centers, a corner of the square and a vertex of the Latin cross are coincident, and the extension of a dashed edge bisects an edge of the cross. The latter two observations identify points at which we can place swing hinges. The swing hinges then get converted to two pieces plus four twist hinges. Also, the piece that gets turned over can be twist-hinged to its neighbors if it swipes an isosceles triangle from each. Note that these isosceles triangles each have one vertex from one small square and another vertex from the other small square.
On page 247, I mentioned a 15-piece 3-way twist-hinged dissection of an octagon to a square to a triangle. If we want a twist-hinged dissection of an octagon directly to a triangle, we can do better. I started with Gavin Theobald's 7-piece unhingeable dissection of an octagon to a triangle, and made some changes to give a 9-piece swing- and twist-hinged dissection. This had five twist hinges and three (hinge-snug) swing hinges. Using my conversion technique from hinge-snug to twist hinges, I got the 12-piece twist-hinged dissection below.
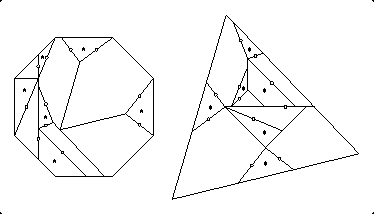
On page 248, I mentioned a 21-piece 3-way twist-hinged dissection of an octagon to a square to a pentagon. Once again, if we want a twist-hinged dissection of an octagon directly to a pentagon, we can do better. I first produced a 13-piece swing- and twist-hinged dissection, using a new pentagon strip as well as the strip I produced for my twist-hinged octagon-to-triangle dissection. My octagon-to-pentagon dissection had nine twist hinges and three (hinge-snug) swing hinges. Using my conversion technique from hinge-snug to twist hinges, I got the 16-piece twist-hinged dissection below.
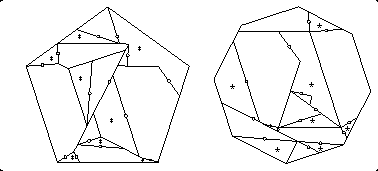
Note that there is a trick that takes some care: The piece on the upper right of the pentagon has had a small right triangle cut out of it, to accommodate two pieces from elsewhere. The shorter leg of this small right triangle is not (and should not be) quite lined up with a side of that piece on the upper right of the pentagon. Thus the piece directly beneath the shorter leg has two sides that are almost lined up, though it does not clearly show this in the above gif figure. Similarly, there is another piece that abuts the pair of almost lined-up sides in the octagon, and thus also has two sides that almost line up.
Gavin Theobald discovered a clever way to modify my 10-piece twist-hinged dissection of a hexagram to a hexagon (Figure 22.46), producing a 9-piece dissection. It causes the small triangle that is attached to the trapezoid to disappear. Gavin split the small triangle into two triangles, with the one that shares an edge with the trapezoid being isosceles. He then glued each of these smaller triangles onto a neighboring piece. Finally, he cut a triangle identical to the nonisosceles smaller triangle out of the center piece and glued it onto the neighboring piece. Very nice swapping around!
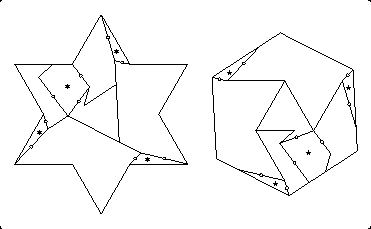
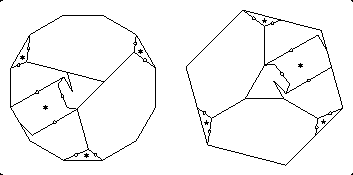
Once I saw Gavin's trick, I realized that it would also work on my 10-piece twist-hinged dissection of a dodecagon to a hexagon, again producing a 9-piece dissection. (I had to undo one trick that I had used for the dissection in Figure 22.50.) To make one piece a bit thicker where a twist hinge is attached, I cut a smaller trapezoid out of the side of the already existing trapezoid, and glued it onto the center piece.
During May-November 2005, I improved the number of pieces for many of my unpublished twist-hinged dissections. I also discovered twist-hinged dissections for pairs of figures that had previously resisted twist-hinging. I described this work in two papers written between November 2005 and March 2006:
- "Unexpected Twists in Geometric Dissections"
- "The Heptagon to the Square, and Other Wild Twists"
Many of these dissections were catalyzed by work on my third book, Piano-hinged Dissections: Time to Fold, because I had discovered a method to convert twist-hinged dissections to be piano-hinged. That discovery prompted me to conduct a more thorough search for good twist-hinged dissections. A listing of many such twist-hinged and piano-hinged dissections appears in Table 4.1 of Piano-hinged Dissections. Of especial note are a 6-piece twist-hinged dissection of a hexagon to a square and a 10-piece twist-hinged dissection of a heptagon to a square.
Robert Reid sent me a nifty twist-hinged dissection of two pentagons plus two pentagrams to a decagon that uses only eight pieces. It is interesting that it uses fewer pieces than the corresponding swing-hinged dissection in Figure 18.9.
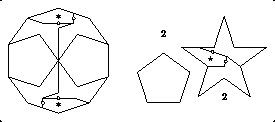
In his 1999 CD-book, Polygons' Combinations, Jean Bauer presented a number of new relationships among polygons. An especially nice one relates the polygons {p} and {2p} for every value of p > 2: There is a dissection of a (2cos(pi / p)-{2p} plus two 1-{p}s to two (1 + 2cos(pi / p))-{p}s.
It is not difficult to find a lovely (2p+2)-piece dissection for this relationship. I have found a corresponding (4p)-piece twist-hinged dissection. I illustrate it for the case of p = 5 below. The decagon plus two small pentagons gives two larger pentagons. Since the two small pentagons are uncut, I have not shown them separately. The use of the rhombus structure of the decagon is self-explanatory. The dissections for other values of p are analogous.
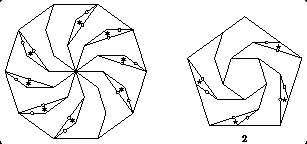
These dissections are included in my paper "Symmetry and structure in twist-hinged dissections of polygonal raings and polygonal anti-rings", which has appeared in the proceedings of Bridges Donostia: Mathematics, Music, Art, Architecture, Culture pp. 21-28, San Sebastian, Spain, July 2007.
In November 2002, I discovered a wonderful family of twist-hinged dissections. Because many things came due at the same time, it has taken me a while to post a few examples of this family. Here they are:
The first is a twist-hinged dissection of a 1-decagon and two (2+phi)-pentagons to a (1+phi)-decagon (Recall that phi is the golden ratio, which is approximately 1.618). Since I don't cut the 1-decagon, I have not shown it separately.
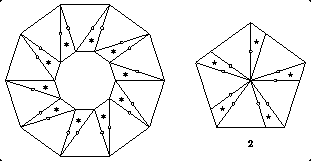
The second is a twist-hinged dissection of a 1-dodecagon and three (1+sqrt(3))-squares to a sqrt(3)-dodecagon. Since I don't cut the 1-dodecagon, I have not shown it separately.
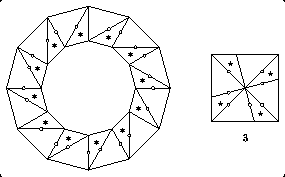
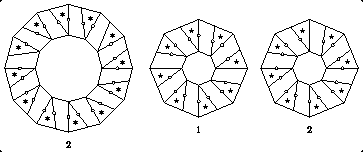
I can also dissect many figures to many. The third is a twist-hinged dissection of two large dodecagons and three small octagons to three large octagons and two small dodecagons. The ratio of the side of the small dodecagon to the side of the small octagon can vary over a wide range, and the sides of the large polygons depend on these values. In the figure below, I chose a ratio of 4:3. Again, I have not shown the uncut polygons separately.
To create such a dissection, we first choose the number of sides in each of the two different polygons: choose p and q to be natural numbers with p> q. We next determine the multiplicity of each type of polygon. Let g = gcd(p, q), the greatest common divisor of p and q. There will be (q / g) number of small {p}s, and (q / g) number of large {p}s, and (p / g) number of small {q}s, and (p / g) number of large {q}s. Next we choose the lengths of the sides of the small polygons: x will be the sidelength of the small {q}, and y will be the sidelength of the small {p}, with y > x >= 0.
Let h = (y - x)/(tan(pi / q) - tan(pi / p)). Let z = (y - x) + 2h tan(pi / p). We can then determine the sidelengths of the large polygons: X = y + z will be the sidelength of the large {q}, and Y = x + z will be the sidelength of the large {p}. We cut the pieces as indicated, and hinge in a greedy fashion: Starting with the first large {p} and the first large {q}, hinge as many pieces as possible from what remains of the current large {q} to fill up as completely as possible what remains of the current large {p}. The number of twist-hinged assemblages will be one less than twice the total number of polygons.
In our example above, p = 12 and q = 8, and g = gcd(12, 8) = 4. Thus there are (8 / 4) = 2 dodecagons of each size, and (12 / 4) = 3 octagons of each size. Once we choose x and y, we can compute values h, z, X, and Y. There will be 9 twist-hinged assemblages: 5 assemblages for the 5 uncut small polygons, and 4 other assemblages, 2 from the outer ring of one large octagon, and one each from the outer rings of the other two large octagons.
When x = 0, we have very small (i.e., no) polygons for that the smaller size of one of the two polygon types. This is the case for either of the first two examples. For the second example, of dodecagons and squares, tan(pi / 4) = 1 and tan(pi / 12) = 2 - sqrt(3). When y = 1, Y = sqrt(3) and X = 1 + sqrt(3).
These dissections are also included in my paper "Symmetry and structure in twist-hinged dissections of polygonal raings and polygonal anti-rings", which has appeared in the proceedings of Bridges Donostia: Mathematics, Music, Art, Architecture, Culture pp. 21-28, San Sebastian, Spain, July 2007.
On page 256, I referred to a 10-piece dissection of a disk to two oval seat tops that have their handholds in the traditional position. Recently, I completely forgot that I had found that dissection, and rediscovered it. So, to help my memory in the future, I supply the 10-piece dissection below. Note that we can get a second 10-piece twist-hinged dissection by changing the position of two of the twist hinges in each oval seat top.
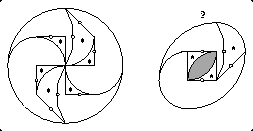
Copyright 2002-2009, Greg N. Frederickson.
Permission is granted to any purchaser of
Hinged Dissections: Swinging & Twisting
to print out a copy
of this page for his or her own personal use.
Last updated January 2, 2009.