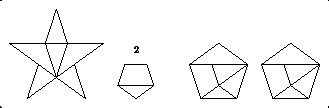
In Ernest Freese's manuscript, Geometric Transformations (completed before his death in 1957), which I got access to in February 2003, there is (in Plate 114) a diagram of the same 9-piece dissection of a dodecagon to three squares as I attributed to C. Stuart Elliott on page 177. So Freese clearly got there first. However his dissection is still not hingeable.
In Ernest Freese's manuscript, Geometric Transformations (completed before his death in 1957), which I got access to in February 2003, there is a dissection of a decagon into two pentagons and two pentagrams, in six pieces. Alfred Varsady rediscovered (rather than discovered) this dissection relation as he explored the families of related dissections in the 1980's and 1990's. Neither man discovered a hingeable dissection for this problem.
In 2001, Jean Bauer noted that there is a propitious relation between a phi-pentagram and two 1-pentagons on the one hand, and two phi-pentagons on the other hand. I have found a 12-piece swing-hingeable dissection, as shown below. How lovely that the pairs of like pentagons are dissected in the same way! Of course, there are 3+2-1 = 4 hinged assemblages, as I also illustrate. It is not surprising that the two phi-pentagons are not hinged in the same way, because we cannot symmetrically divide up the triangles from the pentagram.
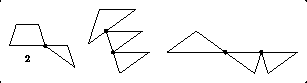
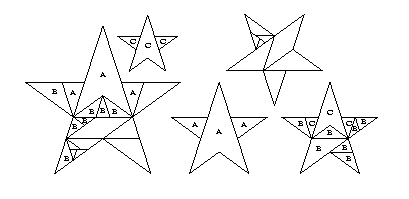
In December 2008, Gavin Theobald wrote that he had found a 1-piece improvement to the multiple pentagram dissection on page 190:"The dissection on figure 18.33 can be improved by one piece. The unlabelled pentagram should be altered by joining the central piece with the two at the top right. This requires an extra piece at the far right of the B-C pentagram."I have redrawn Figures 18.33 and 18.34 to show the result of Gavin's changes. Thus reducing the number of pieces in the unlabeled pentagram by 2 and increasing the number of pieces in the "B-C pentagram" by 1, Gavin has converted my 22-piece dissection into a 21-piece dissection. Excellent!
We can view a hexagram as consisting of twelve small triangles. Adding one more, we get thirteen. Since the square root of 13 can be realized on a triangular lattice, we can get a propitious dissection of a hexagram and a small triangle to a large triangle. It's more interesting to find a hingeable dissection, especially if we are not to be satisfied by a wobbly-hinged dissection. I have found the 8-piece hinged dissection shown below.
Readers may wonder about the mathematical foundations underlying what I call the iso-penta and the iso-hepta triangles. Jean Bauer and Phillipe Lebet have carried out an extensive and fascinating analysis for objects with n vertices, for n = 4, 5, 6, 7, 8, 9, etc. They have developed matrix-based equations similar to those for Fibonacci numbers, they haved derive a myriad of general relationships, they have connected these relationships to the lengths of the diagonals of an n-gon, they have characterized the rhombic structure of the various polygons and stars---all of this in a well-written and beautifully illustrated (in color) CD-based book.
The CD-book, Au delà du nombre d'or (Beyond the Golden Number), by Jean Bauer, Phillipe Lebet, and Stéphane Pécant, was published in 2001 by Trigam sa, 8a puits-godet, CH-2000 Neuchâtel, Switzerland. This new CD-book is a major step beyond the presentation of Jean Bauer's that I list in the bibliography.
Copyright 2002-2003, Greg N. Frederickson.
Permission is granted to any purchaser of
Hinged Dissections: Swinging & Twisting
to print out a copy
of this page for his or her own personal use.
Last updated March 21, 2003.