Jeff Oaks (Mathematics, University of Indianapolis) has pointed out that it is more appropriate to say "Arabic-Islamic civilization" rather than "Arabian-Islamic civilization" on page 51 and "Arabic text" rather than "Arabian text" on page 52. Rather than "Arabian translator" on page 52, I should have written "translator into Arabic". Also, the transliteration al-Khwarizmi is preferred over Alchwarizmi.
Jeff Oaks wrote a paper "Was al-Khwarizmi an applied algebraist?" that caught my attention because it pointed out the mistaken impression that many people have about the House of Wisdom in Baghdad. I wrote to him asking whether Abu'l-Wafa would have had disciples or students. Here is our correspendence on this question.
Here are links for biographical information on the Islamic scholars Thabit ibn Qurra and Abu'l-Wafa.
A fascinating article has appeared that discusses Abu'l-Wafa's manuscript "On the Geometric Constructions Necessary for the Artisan". It is "Mathematics and Arts: Connections between Theory and Practice in the Medieval Islamic World", by Alpay Özdural, has appeared in Historia Mathematica, vol. 27 (2000), pp. 171-201. Follow this link to a webpage with a link to volume 27.
Rick Mabry was kind enough to point out a typo that had escaped notice for more than two decades! In my biography of Abu'l-Wafa al-Buzjani, on page 52, I had left out the 'e' in the word 'translated'. Technically, of course, that 'e' was not lost in translation!
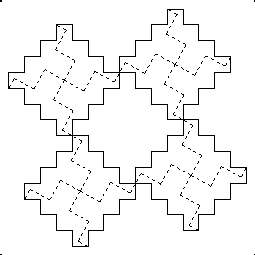
I neglected to attribute the superposition of tessellations in Figure 6.6 to Harry Lindgren (1964b). Martin Gardner had used it in a column that later was collected into The Unexpected Hanging.
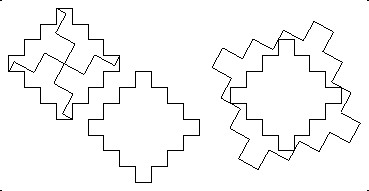
I was rather surprised to discover that Dudeney's 5-piece dissection of two Greek crosses to one generalizes to a family of figures that are sometimes called "stepped crosses". The Greek cross may be viewed as consisting of three rows, the top of which contains one square, which is above a row of three squares, which is above a row of one square. The k-th order stepped cross would have 2k+1 rows, consisting of 1 square in the first row, 3 squares in the second, ... , 2i-1 in the i-th row, up to 2k+1 squares in the (k+1)st row, and then back down. The appropriate generalization of Dudeney's dissection works for any k-th order stepped cross when k is an odd number. Below is the dissection for the 3rd order stepped cross.

The derivation of the dissection is essentially the same as that of two Greek crosses to one: the superposition of tessellations, as we see below. It was not obvious at first that this would work, because one naturally tries to solve the 2nd order stepped cross first and gets all balled up trying to do it in five pieces.
In Ernest Freese's diagrams (from the 1950's), which I got access to late in 2002, there is a diagram for a 12-piece dissection of seven triangles to one. It is different from David Collison's 12-piece dissection, and was almost certainly unpublished earlier than David's was unpublished.(!)
Anton Hanegraaf found a simpler 9-piece dissection of five triangles to one. Since it turns over no pieces, Anton's dissection is preferable to Alfred Varsady's in Figure 6.13. Anton formed a trapezoid with the five triangles and then performed a Q-slide as in Figure 5.3. Note that one cut of the Q-slide coincides with a boundary between two of the five triangles. Thus one of the triangles in the Q-slide comes at little expense. The same approach does not seem to work well for thirteen triangle to three, so that Alfred's two-triangle-to-one technique of Figure 6.12 seems to lead to the best dissection in that case.
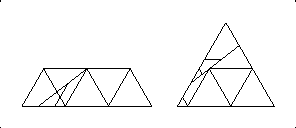
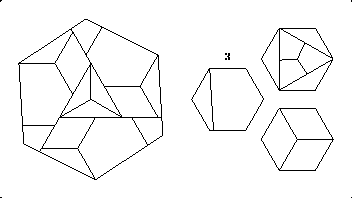
At the top of page 58, I state that the tessellation method doesn't work for five-into-one dissections of hexagons. I meant such tessellations as in Figure 6.15, and had not thought to check tessellation methods such as those in Figures 5.16 and 5.18. Anton Hanegraaf did, and improved on my 16-piece dissection of five hexagons to one in Figure 6.16 by one piece. He combined four hexagons into a large one, in six pieces, and split the fifth hexagon to form two triangles, in four pieces. The superposition of the tessellation of large hexagons similar to that in Figure 5.18 creates just five more pieces, giving a 15-piece dissection. Using the scheme as in Figure 5.16 seems to do no better than 16 pieces. Consonant with one theme in chapter 6, Anton has neatly harvested the fruit of civilizations past.
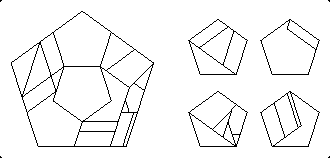
In the spring of 1997, after I had sent my manuscript to the publisher, Robert Reid improved on Alfred Varsady's dissection of six pentagons to one (Figure 6.17). Consonant with the other theme in the chapter, Robert found that a non-tessellation technique produced a 19-piece dissection, an improvement of 2 pieces. The basic idea is to fill out in the large pentagon an area equal to four small pentagons, and then to fill up the remaining area with pieces from the remaining two small pentagons. While preparing a diagram of Robert's dissection, I realized that it could also be improved on, saving yet another piece. My resulting 18-piece dissection turned two pieces over. A year later Anton Hanegraaf saw the dissection on my webpage and modified it so that no pieces need be turned over. A variation of his modification is below.
Copyright 1997-2018, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print out a copy
of this page for his or her own personal use.
Last updated June 7, 2018.