Roberto Doniez found my description of a Q-slide difficult to follow,
and when I looked at it after 17 years, so did I!
I had neglected to state that two edges in Figure 5.4 need to be the same length,
and also did not give an easy way to generate the dissection.
So here is a description that is hopefully easier to follow:
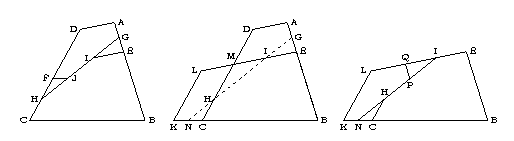
Consider the middle of the figure, which contains quadrilaterals ABCD and BELK, which we would propose to dissect
one into the other.
Note that the quadrilaterals are positioned so that the points B overlap in each,
as do points C and points E.
Place point G on edge AB halfway between points A and E.
Place point N on edge BK halfway between points C and K.
Draw edge GN between points G and N.
Let I be the point at which edges GN and EL intersect.
Let H be the point at which edges GN and CD intersect.
Place point F on edge CD so that F is at twice the distance from C that H is.
Place point J on edge GH so that edge FJ is parallel to edge BC.
Place point Q on edge EL so that Q is at twice the distance from E that I is.
Place point P on edge IN so that edge PQ is parallel to edge EB.
Finally, draw the edges as on the left and right in the figure below.
A 4-piece dissection of a rectangle to a square,
using the Q-slide technique,
appeared in an anonymous Persian manuscript,
Interlocks of Similar or Complementary Figures,
from approximately 1300 C.E.
A more complete discussion of this is included in my second book,
Hinged Dissections: Swinging & Twisting.
The dissection in Figure 5.10 is actually the same as
the dissection in Figure 5.12.
Just rotate everything 120 degrees counterclockwise
in Figure 5.10.
I guess that I liked this one so much
that I just had to show it off twice!
Didn't anyone else do a double take?
In the case of two congruent hexagons to one,
Lindgren's method gives a 9-piece dissection.
In September 2005, Gavin Theobald found a way of performing
the dissection in 8 pieces, if we allow three pieces to be turned over.
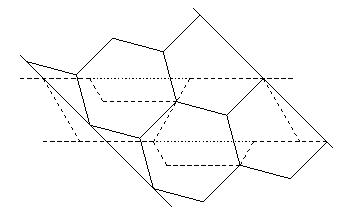
To accomplish this, Gavin used a modified strip dissection.
As shown below,
he created a strip for two congruent hexagons (in solid lines)
and crossed it with a strip for a single hexagon (in dashed and dotted lines).
Choosing the latter strip to be based on lining up two halves of a hexagon,
Gavin found a 9-piece dissection.
But if he extended the rightmost half down to incorporate the dashed trapezoid
beneath it, and thus removed a corresponding trapezoid from the leftmost half,
he avoided cutting one piece in half.
Gavin was careful to accomplish this in a way that allowed the larger half
to mate with the smaller half, after turning over the larger half.
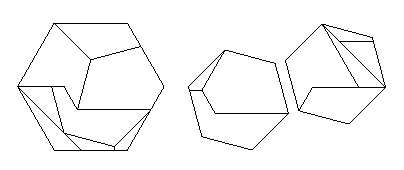
The resulting dissection is below,
with the top three pieces in the large hexagon being turned over.
In the case of two congruent pentagons to one,
Anton Hanegraaf had found a 9-piece dissection with one piece turned over.
In April 2007, Gavin Theobald found a 9-piece dissection with no pieces turned over.
Gavin's dissection uses two applications of the Q-slide technique.
Very neat!
Mike Reid (at Brown University) has pointed out that
there are two pieces turned over in Fig. 5.25 instead of the one
that I claim in the text.
He also pointed out that the text would be correct if we just reflect
the sqrt(3)-hexagram.
Well, I meant to have
my figure reflect the appropriate count.
(This is corrected in the paperback edition.)
Copyright 1997-2014, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print out a copy
of this page for his or her own personal use.
Last updated June 4, 2014.


