Mike Drazin, a mathematics professor at Purdue University, wondered why I had not written a short biography of John Leech. Although Leech seems never to have published his 10-piece dissection of a 6-cube into a 3-cube, a 4-cube, and a 5-cube, it was pivotal in stimulating Roger Wheeler to find his 8-piece dissection. Once I thought about it, I had to agree with Mike. So, better late than never:John Leech was born in 1926 in Weybridge, Surrey, England, and died in 1992. He earned a B.A. in mathematics from King's College Cambridge in 1950. His work on two early computer projects led to a computing lectureship at Glasgow University and eventually a chaired professorship in computer science at the University of Stirling, which he held until early retirement in 1980.Leech is best known for his "Leech lattice" which describes a packing of spheres in 24 dimensions. The packing's symmetry group, identified by John Conway (at Leech's instigation), played an important role in the enumeration of finite simple groups.Although Leech's dissection of cubes may well be lost, he did make another contribution to the sums of cubes: He discovered the smallest number, 87539319, that is the sum of two cubes in three different ways. Apparently, he did not identify a small number of pieces that would form either a 167-cube and a 436-cube, or a 228-cube and a 423-cube, or a 255-cube and a 414-cube.References:
- Anonymous (1992). Obituary John Leech. The Glasgow Herald (October 1).
- Leech, John (1957). Some solutions of Diophantine equations. Proceedings of the Cambridge Philosophical Society 53 778-80.
- Munn, Walter Douglas (1992). John Leech: Navigator of maths. The Guardian (October 14), London.
- Silverman, Joseph H. (1993). Taxicabs and sums of two cubes. American Mathematical Monthly 100, 331-40.
- Thompson, Thomas M. (1983). From Error-Correcting Codes Through Sphere Packings to Simple Groups. Mathematical Association of America: Washington.
Willem van der Poel, at the Technical University in Delft, the Netherlands, informed me that he had a student Edo Timmermans who wrote a computer program to find 8-piece dissections of cubes for 33 + 43 + 53 = 63. The program produced thousands of distinct solutions. Willem chose one of the solutions from which he constructed his exchange puzzle at the 15th International Puzzle Party, in 1995.
In 2000, Timmermans focused on identifying solutions that make challenging assemble/disassemble puzzles, and conducted further computer searches. Not only did he find solutions in which some of the pieces must be slid against each other along specific trajectories, but some pieces must be rotated relative to each other. Timmermans has described these results in:The last of these articles is especially fascinating, with the "holy trinity puzzle" having lovely properties, including three different types of movement to disentangle the pieces. Check out Edo's lovely wooden model in my photo gallery.
- "The Trinity Puzzle," Cubism for Fun, No. 56 (October 2001) pages 4-5.
- "The Trinity Puzzle (2)," Cubism for Fun, No. 58 (July 2002) pages 22-24.
- "The Trinity Puzzle (3)," Cubism for Fun, No. 60 (March 2003) pages 10-11.
- "The Holy Trinity Puzzle," Cubism for Fun, No. 62 (November 2003) pages 26-29.
Brian Trial has sent me a dissection of cubes for 33 + 43 + 53 = 63 that has an interesting property. In moving pieces from the 3-, 4-, and 5-cubes to the 6-cube, pieces are rotated around a single axis, not all three. This axis is perpendicular to the levels as Brian displays them below. Brian's dissection uses ten pieces. He asked whether there is a 9-piece dissection that satisfies the rotation constraint.

Brian came to formulate this constrained problem because he was using his son's Legos to construct the cubes. I observed that his dissection would allow us to make a model out of wood such that the grain of the wood is aligned in both the 6-cube and the set of 3-, 4-, and 5-cubes. (Just orient the grain in the same direction as the single axis of rotation.) The grain preserving property is more general, however, since it also allows us to flip the pieces upside down too.
In the summer of 2003, Edo Timmermans found several more 8-piece solutions for cubes for 33 + 43 + 53 = 63 that have some interesting properties. They are grain-preserving, but cannot be separated in three dimensions. If one cuts two 1-cubes off of a certain piece, then the resulting set of ten pieces can be separated. Edo wrote in a follow-up message:I consider the existance of this puzzle an indication that separable cases with 8 pieces do exist, I just have to find them by writing a program with different restrictions.
In February of 2005, Edo Timmermans informed me that had found 8-piece solutions for parallelopipeds for 33 + 43 + 53 = 63. These correspond to a corresponding translational dissection for cubes. They are described in the following article:Check out Edo's nifty model in my photo gallery.
- "Shape Shifting Trinities," Cubism for Fun, No. 66 (March 2005) pages 10-13.
In early 2005, Edo Timmermans informed me that had found 8-piece solutions for cubes for 33 + 43 + 53 = 63 in which two pieces cannot be disentangled, though they can be rotated and shifted relative to each other. Check out Edo's interlocking model in my photo gallery.
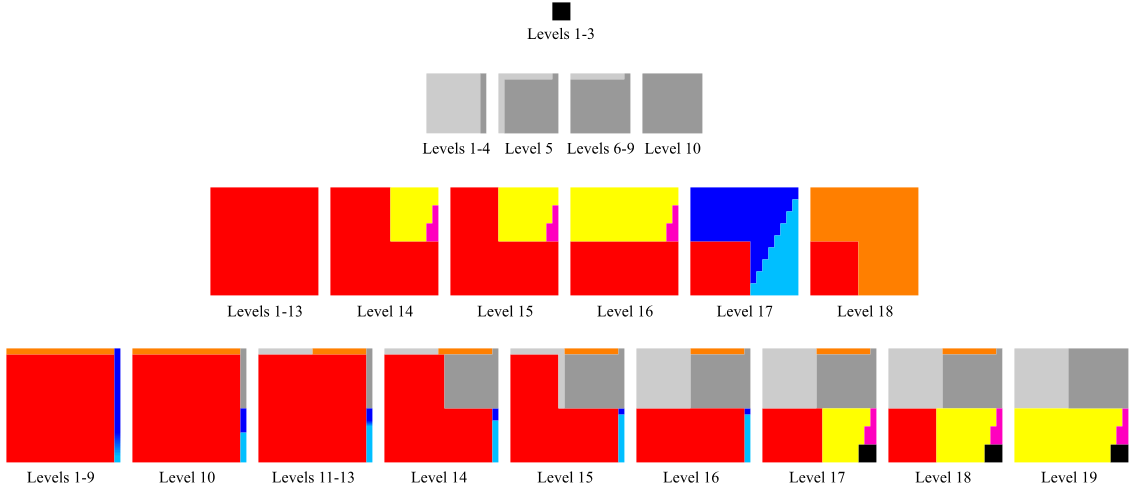
In 2009, I published an article on generalizations of Robert Reid's dissection of cubes for 13 + 13 + 53 + 63 = 73:Greg N. Frederickson, "Casting light on cube dissections," Mathematics Magazine, vol. 82, no. 5 (December 2009), pp. 323-331.This was a new infinite class of number identities, starting with Robert's identity:
13 + 13 + 53 + 63 = 73
13 + 13 + 23 + 23 + 163 + 173 + 183 = 193 + 203
13 + 13 + 23 + 23 + 33 + 33 + 333 + 343 + 353 + 363 = 373 + 383 + 393
etc.
Each dissection of cubes uses an arguably minimum number of piece, just as Robert's does. Also included in the article are symmetric dissections of cubes for these identities that use just one more piece each. In addition, I present other identities and their associated cube dissections. Check it out!
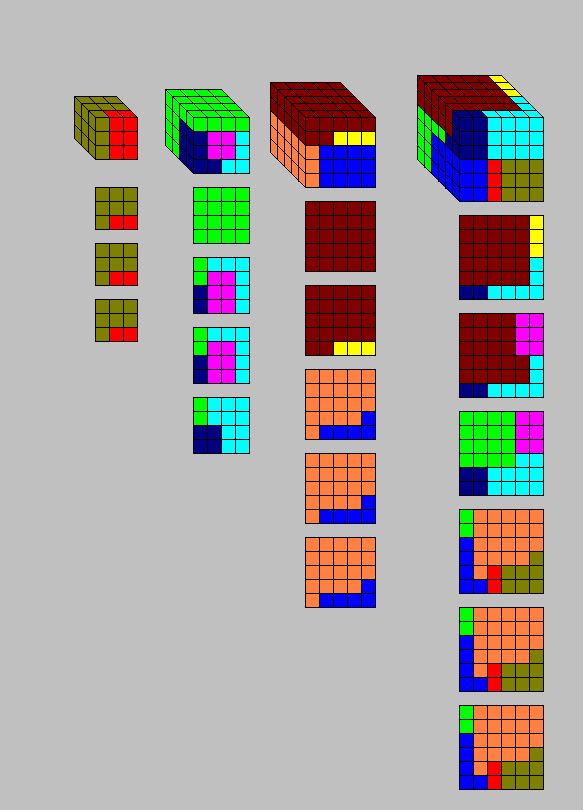
In November 1999, Robert Reid improved on his 11-piece dissection of cubes for 23 + 163 = 93 + 153 that I had mentioned in my book. He saved one piece, producing a 10-piece beauty that is at most one piece over the minimum needed for any rational dissection of this set of cubes.
Below are the level by level diagrams for the 9-cube and the 15-cube. Most remarkable is Robert's use of what he calls the corkscrew. Piece I is a corkscrew. (That makes piece E the cork, I guess.) As we move the pieces into the 16-cube, piece I will rotate a quarter-turn in the clockwise direction, and will shift down two levels, with respect to piece E. Also, piece B is a corkscrew, with piece A the cork. As we move the pieces into the 16-cube, piece A will rotate a quarter-turn in the counterclockwise direction, and will shift up two levels.
Below are the level by level diagrams for the 16-cube. (The 2-cube is a single piece, piece J, for which I have not given level by level diagrams.) Since Robert used two corkscrew pieces, he called it the double-corkscrew technique. I wonder how well it works on wine bottles....
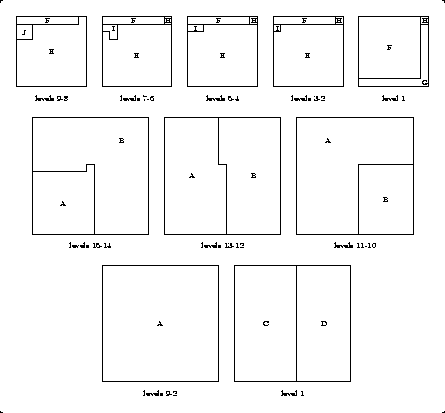
On the other hand, Gavin Theobald improved on Robert Reid's 10-piece dissection of cubes for 33 + 103 + 183 = 193 that I had mentioned in my book. He also saves one piece, and produces a lovely 9-piece dissection that is at most one piece over the minimum needed for any rational dissection of this set of cubes.
When Gavin sent me the above cube dissection, I realized that I had forgotten about Robert Reid's 9-piece improvement on cubes for 33 + 103 + 183 = 193, which he had sent me in January 2003. Thus we now have two competing 9-piece dissections. This provides some hope that an 8-piece dissection might be possible.
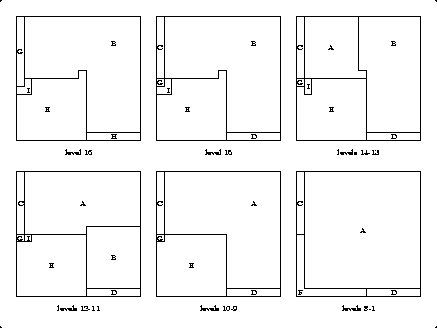
The 3-cube and the 10-cube are uncut. Below are the level by level diagrams for the top 9 levels of the 18-cube. The bottom 9 levels of the 18-cube involve just piece D, and are thus not shown.
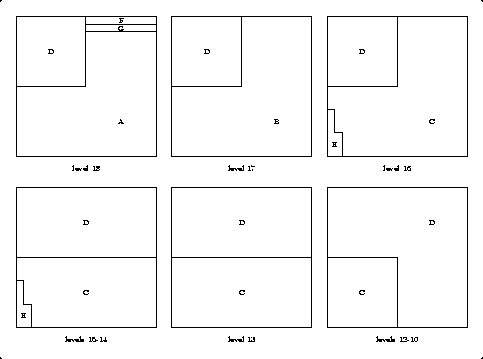
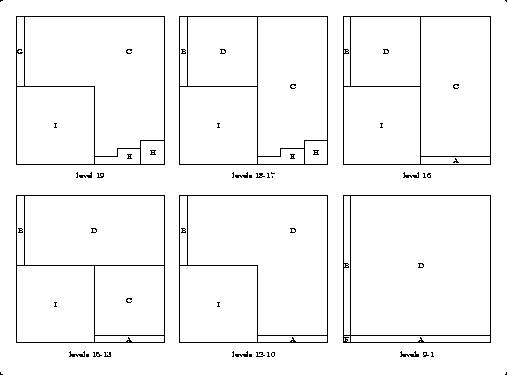
Below are the level by level diagrams for the 19-cube. We see that Robert once again used the corkscrew technique, with piece C being the corkscrew and piece D the cork. Moving from the 18-cube to the 19-cube, we must rotate the corkscrew one quarter-turn counterclockwise, as it shifts down three levels. Note that pieces A and B in the 18-cube were cut from what would have been the bottom two levels of the corkscrew. Robert also uses a steplike piece E, which he shifts over to produce a cavity for the 3-cube (piece H).
We have seen hole dissections for rectangles and squares on pages 65-66, in which a rectangle with a rectangular hole is converted to a square. A folding version of such puzzles was presented in chapter 7 of my book Hinged Dissections: Time to Fold!. Now Edo Timmermans had attacked the problem of dissecting a rectangular solid with a hole in the form of a rectangular solid to a cube in"Hidden Hole Dissection," by Edo TimmermansIdeally, we would like the hole centered in each of the three dimensions. Edo achieves this with a dissection of a 4x7x8 rectangular solid with a 2x1x4 hole to a 6-cube, where indeed the hole is hidden. Edo also achieves a dissection of a 4x7x8 rectangular solid with a 4x1x2 hole to a 6-cube. In this case, the hole goes all the way through the rectangular solid.
Cubism for Fun, no. 79 (July 2009), pp. 21-24.
Edo also presents such variants as a rectangular solid with a hole in the form of a rectangular solid to a rectangular solid ((4x4x7)-solid with 2x2x1 hole) and a rectangular solid with an off-center hole to a cube.
All the dissections in Edo's article use just four pieces--the minimum possible under a very reasonable assumption. Also, there are several with lovely symmetry.
My thanks to Brian Trial, Gavin Theobald, and Robert Reid,
who have granted me permission to display their dissections.
Everything else is copyright 1999-2017, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print out a copy
of this page for his or her own personal use.
Last updated March 28, 2017.