Ernst Specker, an emeritus professor of mathematics at ETH in Zürich, pointed out what seems to be a problem in the second paragraph of my introduction. I wrote thatthe problem was solved before the congress even got under way.but this relies on a somewhat sloppy interpretation of the German word "inzwischen" in a footnote. Did Hilbert mean "between the time when his paper was written out (prior to the congress) and the time when it was presented"? Or did Hilbert mean "between the time when his paper was presented at the congress and the time when it was printed"? Absent more explicit information, I would now opt for the latter, more conservative, interpretation. So I should probably have written:the solution was in print just two months after Hilbert's address.
Bernhard W. Marx has pointed out that the parameter r relating to a Hill tetrahedron of the first type, as discussed on page 233, should have an upper bound of sqrt(3), not sqrt(2).
My choice of example for Anton Hanegraaf's dissection of two cubes to one was unfortunate: I forgot that when x/y = 1/2, Anton had found a 10-piece dissection, replacing pieces F, G, and H in Figure 20.12 by two pieces. The 11-piece dissection in the figure is appropriate if we take, for example, x/y = 499/1000. So let's assume that the figure illustrates that case.
I neglected to reference David Paterson's (1988) dissection of a rhombic dodecahedron to a cube. His P-strip dissection used 15 pieces. (Sorry for the oversight, David.)
In Mathematical Questions and Solutions from "The Educational Times", volume 17 of the second series (1910), pages 19-22, a solution is given to James Blaikie's problem of dissecting one truncated octahedron into five pieces that form a rectangular solid whose length and breadth are each equal to twice its height. Actually, the dissection can be accomplished in four pieces, using the top half of the cube in Figure 20.13. The truncated octahedron is cut into four identical pieces as on the left in that figure.
James Andrew Blaikie was born in Edinburgh, Scotland in 1847. At Cambridge University he earned a B.A. and an M.A. in mathematics. He was Mathematical Master at Fettes College, Edinburgh, from 1870-76, Inspector of Schools for Edinburgh, 1877-86, Examiner to the Scottish Education Department, 1886-89, and was afterwards examiner for the Civil Service Commission and the Board of Education Examinations. He wrote textbooks on dynamics (mechanics) and geometric deductions. Blaikie was a fellow and examiner of the British Esperanto Association and was also interested in botany, stamp-collecting, and mountaineering. He died in 1929.
Dissections involving combinations of Platonic and Archimedean polyhedra have been proved to be possible by J. H. Conway, C. Radin, and L. Sadun in their article "On angles whose squared trigonometric functions are rational", Discrete & Computational Geometry, 22 (1999), pages 321-332. For instance, they argue that that there is a dissection of a dodecahedron, an icosahedron, and an isosidodecahedron, all of the same edge length, into a finite number of pieces that form a cube. The authors admit that they have no idea how to actually perform such dissections.
Anton Hanegraaf points out that there is a large list of rectifiable polyhedra (proved to be dissectible to a prism by the criterion of Dehn), for which actual dissections are still unknown. See for instance the list of rectifiable tetrahedra in Hilbert's Third Problem by Boltianskii (1978) pages 170-173. Apart from the tetrahedra of Liu, Haüy and Hill, for which dissections to prisms now are known, the list contains 25 tau-tetrahedra (related to the rhombic triacontahedron) for which dissections to prisms are still not known. Note that the list of Boltianskii is not complete! One of the most promising of the list is the trirectangular tau-tetrahedron, which is obtained by taking a 1/120 part of a rhombic triacontahedron. Sydler (1956) proved that this tetrahedron is rectifiable. He provided an actual dissection to a group of rectifiable polyhedra. His dissection involves hundreds of pieces, so a drastic reduction of pieces is desirable.
Gavin Theobald has improved on Anton Hanegraaf's dissection of a truncated octahedron to a cube, down to 12 pieces. When Gavin told me of his dissection, he challenged me to see if I could find it. I got nowhere on that one and eventually turned the page to work on Anton's dissection of a rhombic dodecahedron to a cube. I had more luck with this one, and improved it by one piece. On hearing this, Gavin admitted that he had spent "ages" trying to improve Anton's 13-piece dissection. If great minds run on parallel tracks, what kind of minds run on perpendicular tracks?
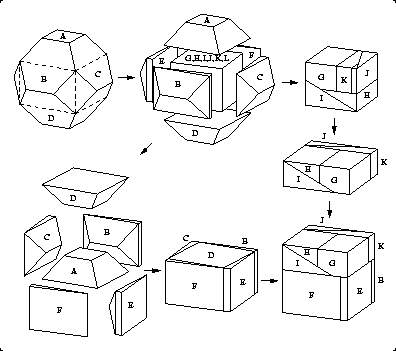
Below is Gavin's dissection of a truncated octahedron to a cube. It is an ingenious adaptation of Anton's approach in Figure 20.14. Like Anton, Gavin cuts away the top and bottom (pieces A and D), and also the four sides (pieces B, C, E, and F). But he attaches triangular prisms to these four sides, so that pieces A through F can be assembled into a rectangular block whose length and width are already that of the desired cube. The interior of truncated octahedron is a rectangular block. It can be converted to a rectangular block that fills out the rest of the cube, much as Anton did, using two P-slides. The 12th piece (piece L) is the unlabeled small wedge-shaped piece.

Gavin's insight is that pieces B, C, E, and F can be extended into the interior of the truncated octahedron so as to fill out to the boundaries of the cube. Looks easy, but only by hindsight! Gavin also noted that his approach works nicely to give a 12-piece dissection of a stellated rhombic dodecahedron to a cube.
In October 2007, Gavin Theobald went one better and found a dissection of a truncated octahedron to a cube, in only 11 pieces. It's a 3D version of a strip dissection that can be accomplished using only four slices. It's really hard to visualize these dissections, so we don't yet have a good diagram to display it. Stay tuned...
Below is my dissection of a rhombic dodecahedron to a cube, which is produced by rearranging and swapping portions of pieces in Figure 20.15. To convert that figure to this diagram, do the following. First, switch the names of pieces L and M. Then turn the rectangular block (pieces K, L, and M) in the cube on the lower left so that the wedge-shaped piece K (label not shown) sits on top on the right. Next, switch pieces C and D in the cube; this is easy since they are the same. Now attach the new piece M (old L) to piece D, as shown in the top right (and bottom right too). To have this new D fit in the rhombic dodecahedron, cut a piece (in the shape of the old L) out of A, as in the lower right. To fill in the space in the cube caused by trimming A, add a piece (in the shape of the old L) to G, as in the lower left. In the rhombic dodecahedron, the new G is the union of the old G and the old L, as in the lower middle. Thus we have disposed of the thirteenth piece (the old L, or new M).
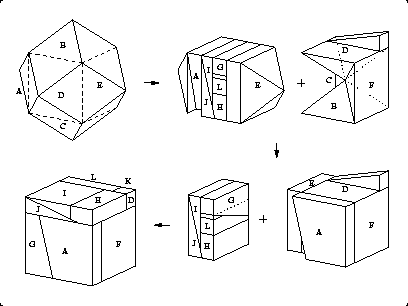
Gavin has also produced a 12-piece dissection of a stellated rhombic dodecahedron to a cube. It is closely related to his dissection of a truncated octahedron to a cube.
In October 2007, Gavin Theobald went one better and found a dissection of a rhombic dodecahedron to cube, in only 11 pieces. It's a 3D version of a strip dissection that can be accomplished using only four (or is it five?) slices. Actually it looks like Gavin used a customized strip. But it's really hard to visualize this dissection, so we don't yet have a good diagram to display it. Stay tuned...
Anyone who has taken the time to contemplate Anton Hanegraaf's wonderful Delian Altar Dissection booklet must be in awe of Anton's geometric skills. Once that I told him of my plan for a second book (on hinged dissections) he was enthusiastic and supportive in the extreme. As I describe in my second book Hinged Dissections: Swinging and Twisting, he was the inspiration behind the T(a)-swing and its use in two dissections from that book's chapter 3, ten more hinged plane dissections, and also much of the chapter dealing with hinged dissections of 3-dimensional figures. Amazing stuff! After a long illness, Anton Hanegraaf passed away on September 28, 2001.
Gavin has also improved Duilio Carpitella's 16-piece dissection of an octahedron plus two tetrahedra to a cube. Gavin has gotten it down to fifteen pieces.
Finally, Gavin has improved on Duilio Carpitella's 28-piece dissection of a truncated octahedron to rhombic dodecahedron. Gavin has produced a wonderfully symmetric 24-piece dissection. I will have to get my act together and reproduce these last two dissections here.
In October 2007, Gavin Theobald found an 8-piece dissection of a regular hexagonal prism (with hexagonal and square faces) to a cube. It uses a strip technique and produces all convex pieces. In fact, it is possible to cut the hexagonal prism into the eight pieces by using only slices that go completely through whichever piece you are cutting.
In November 2008, Gavin Theobald sent me dissections of three more regular prisms to cubes. They are a 10-piece dissection of a regular triangular prism to a cube, an 11-piece dissection of a regular heptagonal prism to a cube, and an 11-piece dissection of a regular octagonal prism to a cube. The latter two involve using a strip technique to get a rectangular block of width equal to the length of the cube, then chopping off a smaller rectangular block to leave a square rectangular block, and finally applying a P-slide to the smaller rectangular block to get a square rectangular block to stack with the previous one.
Copyright 1997-2013, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print out a copy
of this page for his or her own personal use.
Last updated March 27, 2019.