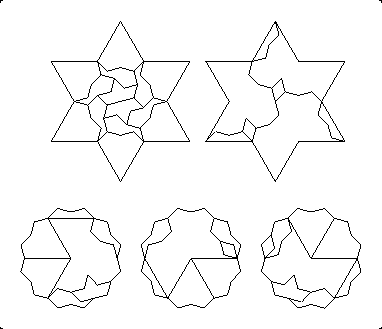
Soon after I sent the final manuscript of my book off to the publisher in January 1997, Robert Reid improved three {12/2}s to two {6/2}s (Figure 18.6), from 23 pieces down to 22. Two pieces are turned over.

Anton Hanegraaf has pointed out that my approach for dissecting a {7/3} to a heptagon (Figure 18.7) needs at most 13 pieces. The conversion of an isosceles triangle in the {7/3} to an irregular triangle in the heptagon needs only three rather than four pieces. I just crossposed the T-strips in the wrong way. Interestingly, the general version of the resulting dissection of two triangles of equal height was identified by Henry Taylor in his 1905 paper.
In Ernest Freese's manuscript, Geometric Transformations (completed before his death in 1957), which I got access to in February 2003, there is a dissection of a decagon into two pentagons and two pentagrams, in six pieces. This is essentially the same as the dissection in Figure 18.10. Thus Alfred Varsady rediscovered (rather than discovered) this simple dissection as he explored the families of related dissections in the 1980's and 1990's.
When I was asked to make suggestions for the dust jacket of my book, I found something rather nice. The pieces in the middle-sized {7/2} of Figure 18.23 can be cyclicly hinged. This also works for the analogous dissections involving {9/2}, {11/2}, etc., but unfortunately not for the {5/2} dissection of Figure 18.22. Too late to make it into the book, this observation survives in the illustration on the front cover of the dust jacket - a good reason not to toss it out!
As I noted in the updates to Chapter 9, the approach of the Tri-root class for hexagons can be extended to octagons, decagons, and so on. (See Tri-root class extended to octagons, decagons, etc..) Since we already have a class for {5 / 2}, {6 / 2}, {7 / 2}, and so on, it would be nice if we could extend the other way, to additional dissections for each such star. And so we can. In September 1998 I generalized this group of dissections so that there are (2m+1)-piece dissections of {m / 2}s for y / x = n tan (2 pi / m) for every whole number n. Furthermore, in early October 1998, I generalized the group of dissections so that there are (2p+1)-piece dissections of {p / q}s for y / x = 2n cos ((q-1) pi / p) sin ( pi / p) / cos (q pi / p) for every whole number n. These are described in my new book Hinged Dissections: Swinging and Twisting.
In analogy to the golden ratio, I defined the "silvern ratio" as 2cos(pi/7) on page 218. Alternatively, we can define it as the solution to the equationy3 - y2 - 2 y + 1 = 0In the afterward, I noted that Tutte had defined the "silver number" as the square of the silvern ratio. In his column, "Tales of a Neglected Number," Scientific American (June 1996). pages 92-93, Ian Stewart defined the silver number as the solution to the equationy3 - y - 1 = 0This gives a value of approximately 1.324717957, different from my silvern ratio and Tutte's silver number. I guess this just confirms that silver is more common than gold.
Readers may wonder about the mathematical foundations underlying what I call the iso-penta and the iso-hepta triangles. Jean Bauer and Phillipe Lebet have carried out an extensive and fascinating analysis for objects with n vertices, for n = 4, 5, 6, 7, 8, 9, etc. They have developed matrix-based equations similar to those for Fibonacci numbers, they haved derive a myriad of general relationships, they have connected these relationships to the lengths of the diagonals of an n-gon, they have characterized the rhombic structure of the various polygons and stars---all of this in a well-written and beautifully illustrated (in color) CD-based book.
The CD-book, Au delà du nombre d'or (Beyond the Golden Number), by Jean Bauer, Phillipe Lebet, and Stéphane Pécant, was published in 2001 by Trigam sa, 8a puits-godet, CH-2000 Neuchâtel, Switzerland.
In January 2021 I realized that the dissections of pentagrams for (sin 2*pi/5)2+(cos 2*pi/5)2 = 12 and of heptagrams for (sin 2*pi/7)2+(cos 2*pi/7)2 = 12, in Figs. 18.22 and 18.23, resp., could be generalized for any star {(2m+1)/2}, where m>3. There should be a corresponding (4m+3)-piece dissection displaying the relation (sin 2*pi/(2m+1))2+(cos 2*pi/(2m+1))2 = 12. In particular, for m=4, there would be a 19-piece dissection of enneagrams (i.e. {9/2}s} for(sin 2*pi/9)2+(cos 2*pi/9)2 = 12.I plan to display an illustration of this one here, hopefully soon.
Copyright 1997-2021, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print out a copy
of this page for his or her own personal use.
Last updated January 19, 2021.