In Ernest Freese's diagrams (from the 1950's),
which I got access to late in 2002,
there is a diagram of the same 10-piece dissection
of a {10/3} to two {5/2}s as in Figure 16.2,
which I had (implicitly) attributed to Harry Lindgren.
Freese also had an 8-piece dissection
of an {8/2} to two {4/1.5}s,
but did not make a claim about there being an infinite
class of such instances.
There is a typographical error in the first paragraph on page 173.
In the sentence that begins,
"Lindgren split ...",
it should read "decagon" rather than "pentagon".
There are several typographical errors in the paragraph on page 173
that begins:
"An equally masterful dissection ..."
The third sentence should read:
"The ratio s{5/2}/r{10/3} = sqrt(2)
between the side of the pentagram
and the short radius of a {10/3} of equal area
makes this dissection possible."
The last sentence of that paragraph should read:
"... such as two {3}s to one {6},
and two {7/3}s to one {14/5}."
(The last sentence is corrected in the paperback edition.)
There is a related typographical error in the last paragraph on page 179
that begins:
"Galaxy (16.7) has auspicious dissections of two ..."
The next expression should read "{(4n+2)/(2n-1)}s"
rather than "{(4n+2)/(n+1)}s".
This makes it consistent with line (16.7) of the first table.
(This was supposed to be corrected in the paperback edition,
but the change was unfortunately made to the sentence that begins
"Galaxy (16.5) has auspicious dissections of ...",
thus rendering both sentences incorrect!)
In the second paragraph on page 177,
replace "simple two-to-one dissections" by "simple one-to-one dissections".
Missing Heptagram Dissection
Gavin Theobald has drawn my attention to what looks like a spurious claim that I made
in the sentence that starts at the bottom of page 175 and then continues on page 176.
The claim is that there exists an 11-piece dissection of a {14/2} to a {7}.
On his webpage "Heptagon Dissections", Gavin displays a 12-piece dissection that he identifies as "a modification of a dissection found by Greg Frederickson." I vaguely recall that I had such a dissection, but a frantic search of my (20-year-old) records from around the time that I published the book hasn't turned up a picture of either an 11-piece or a 12-piece dissection. Gavin concludes (about me) that: "Either he miscounted the number of pieces, or there is a forgotten trick to save a piece." I wonder which it is.
Koji Miyazaki, Hirohisa Hioki, and Naoki Odaka
examined my tables on pages 174-175 and 181
and found a number of mistakes:
Equation (16.7) on page 175 should have the numerator and denominator interchanged.
Equation (16.8) on page 175 should have R{(8n-2)/(2n-1)} rather than R{(8n-2)/(2n)}.
Equation (16.11) on page 175 should have an extra factor of 2 on the righthand side.
Equation (16.13) on page 181 should have the 2 replaced by sqrt(2) on the righthand side.
Equation (16.18) on page 181 should not have
that factor of 2 on the righthand side.
Equation (16.19) on page 181 should have
an additional factor of 2 on the righthand side.
On page 179, I note that Harry Lindgren (1964) gave a 4-piece dissection
of a hexagon to two triangles.
This appears to have been known much earlier,
because it seems to have been described briefly by Leonardo da Vinci
(1452-1519)
in one of his notebooks.
On Foglio 122 (volume 2) of the Codex Atlanticus,
Leonardo sketched a hexagon,
inscribed a triangle inside of it,
and cut the triangle into three pieces
identical to the portions of the hexagon outside of the triangles.
He labeled this drawing with the following (in Italian):
El triangolo che con li sua angoli è contingente
alli 3 angoli dello esagone, vale la metà d'esso
esagone.
which translates as:
The triangle that with its angles is contingent on the 3 angles
of the hexagon is the same as half of this hexagon.
See the updates to my preface for the full reference
to the transcription and facsimile reproduction of Codex Atlanticus.
On page 181 I listed those trigonometric relationships between stars (and polygons)
that seemed to be of no general pattern.
One of those was the relationship (16.13),
corrected in an earlier entry on this webpage as:
r{10/4} / r{5/2} = sqrt(2) cos(π /5)
On the next page I mentioned that Harry Lindgren gave an 18-piece dissection
of two {5/2}s to one {10/4}, which I reproduced as level 2 of the prism dissection
in Figure 22.8.
It turns out that the relationship between
one {10/4} and two {5/2}s
is not an isolated curiosity
but the first in an infinite sequence.
For every positive n, we have that
s{ (8n+2) / (2n+2) } / s{ (4n+1) / (n+1) } = sqrt(2) cos( (π / 2)(2n+1) / (4n+1) )
Note that I express the relationship in terms of the ratio of the side lengths,
rather than the ratio of the r parameters,
the shorter of the two radii for a star.
This seems more natural, allowing us to use the law of sines and the formula
for the sine of a double angle to simplify the ratio.
We can then plug in the first several values of n to identify the first few cases.
For n = 1, we get Harry's two {5/2}s to one {10/4}.
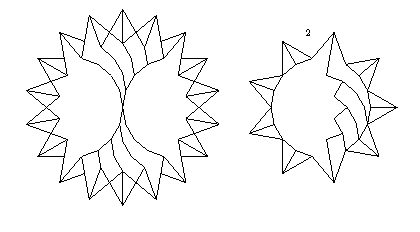
For n = 2, we have two {9/3}s to one {18/6}.
For n = 3, it's two {13/4}s to one {26/8}.
And so on.
There are natural dissections for each case,
with the nth dissection using 16n+2 pieces.
For the case n = 2 we see below the 34-piece dissection:
Project Runeberg
maintains a database on Nordic authors.
The biographical information for
Harry Lindgren
focuses on his work related to English spelling reform.
In 2017 Amanda Laugesen published an article, "Lindgren, Harry (1912-1992)", for the
Australian Dictionary of Biography.
Follow the link to Harry's biography.
Copyright 1997-2014, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print a copy
of this page for his or her own personal use.
Last updated January 15, 2019.
