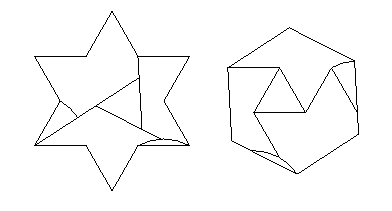Robert Macmillan wrote that
when he went down to Emmanuel College in 1941,
he came to know G.T. Bennett for a short while
before the latter's death.
Bennett was popularly known then as "Beaver" Bennett,
because he had a formidable white beard in his old age.
Macmillan explains that in Britain in the 1930's
a beard was called a "beaver", although he does not know why.
Perhaps this usage comes from an alternate meaning for beaver,
deriving from the Middle English "baviere", which came from Middle French,
which was a piece of armor protecting the lower part of the face.
When Henry Dudeney posed the problem of dissecting an
octagon to a square,
in his "Perplexities" column in the Strand Magazine,
volume 71 (1926), page 416,
he stated that he believed that no such dissection
had ever been published.
But the problem of dissecting an octagon to a square in as few pieces as possible
was posed earlier by James Blaikie
in Mathematical Questions and Solutions from "The Educational Times."
In response to his challenge,
Henry Martin Taylor gave an 8-piece dissection in
that periodical in
volume 16 of the second series (1909), pages 81-82.
Thus Henry Dudeney's 7-piece dissection,
which he gave in the Strand Magazine,
volume 71 (1926), page 522,
was an improvement of one piece over the earlier dissection.
Both dissections converted the octagon to a rectangle and then
performed a P-slide.
Dudeney's conversion avoided one additional crossing of cuts.
The lovely 5-piece dissection of an octagon to a square
appeared much earlier, in an anonymous Persian manuscript,
Interlocks of Similar or Complementary Figures,
from approximately 1300 C.E.
A more complete discussion of this is included in my second book,
Hinged Dissections: Swinging & Twisting.
Harry Lindgren wrote in a 1963 letter to C. Dudley Langford that
Ernest I. Freese was a partner in the
architectural firm Boyle, Meldt & Freese.
The firm is almost certainly bogus,
its name exploiting a pun on the name Freese.
So who was responsible for this bit of fun?
Take another look at Freese's biography and see if you can guess!
Also, check out Ernest Irving Freese's photograph and "autobiography"
(approx 46K).
From Pencil Points, vol. 11 (1930) page 224.
An earlier example of his humor appeared in
"A Bungle-Ode,"
by Ern. Freese,
in The Architect and Engineer of California, March 1918.
Freese's 5-part series on perspective projection
was also published as a 43-page book,
Perspective Projection; a Simple and Exact Method of Making Perspective Drawings,
Pencil Points Press, New York, 1930.
If you examine the bibliography of this first book, you will find the following entry:
"Freese, Ernest I. (1957). Blueprints containing over two hundred plates.
Described briefly in letters by C. Dudley Langford and Dorman Luke.
Complete copy not located."
As I was writing my first book, I was lucky to have had Judy Lindgren offer to search through
the correspondence of her father Harry to identify letters that mentioned geometric dissections.
One letter to Lindgren noted Freese's address before he passed away in 1957.
Hoping that Freese's wife Winifred might still be alive, I mailed a letter to the address
where she and her husband had lived almost four decades earlier.
Although Mrs. Freese had by that time passed away,
her son Bill was still living in that very same house and answered my letter!
Unfortunately, the son did not know if any of his father's work on dissections had survived,
but he said that he would look.
After not hearing from him for a year,
I wrote another letter, addressed to him this time, but got no further response from him.
However, in 2002, when Bill entered a hospice for cancer patients,
his cousin Vanessa Kibbe, who was his designated heir, started to clean out the house.
She found an unopened letter from me to Bill,
which alerted her to the existence and significance of the manuscript.
Within a few months she had located that legendary tome!
In 2003 I flew out to Los Angeles to make a copy of the manuscript
as well as many other documents that Vanessa had located and set aside for me.
Once I got home, I worked off and on to electronically clean up the copy, wrote an extensive commentary of the manuscript,
including a summary of Freese's life, as well as improvements on and extensions to Freese's dissections.
I also found a publisher, World Scientific Publishing, that was willing to put out a 400-page,
oversize book:
Ernest Irving Freese's 'Geometric Transformations': the Man, the Manuscript, the Magnificent Dissections!, 2018.
Using the completing the tessellation technique,
Wolfgang Stöcher has designed a very pretty
dissection of a regular hexagon to an equilateral triangle (stale link).
Since it has 7 pieces, it is not minimal.
But it has 3-fold rotational symmetry
and thus is really attractive.
Of especial interest, the two small triangles that are added
each have sidelength one half of that of the large equilateral
triangle.
I know of no other example of completing the tessellation
for which the side of an added polygon is one half the side
of one of the given polygons.
In March 2007, Gavin Theobald discovered a way to modify
my 6-piece hexagram-to-hexagon dissection so that no pieces
need be turned over.
He enlarged the two triangles that are turned over
so that each resulting piece has mirror symmetry
and thus need not be turned over.
He did this by introducing curved cuts,
so that one piece becomes a "pie slice"
and the other is the portion of a circle cut
off by a chord.
The circular cuts have a radius equal to the length
of the edge of the hexagram.
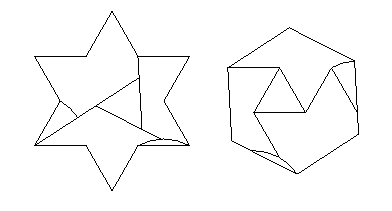
The "chord slice" is also an improvement
in that it is a considerable enlargement of the tiniest
piece, which had been somewhat of a blemish on the dissection.
As far as I know,
this is the first essential use of circular cuts
in a dissection whose figures do not have curved boundaries.
Really nifty!
Martin Gardner wrote a column on geometric dissections
in Scientific American in 1962,
and gave a table that listed the number of pieces that suffice
for various dissections.
Noting that there was no entry for the hexagram to hexagon,
then-20-year-old Bruce R. Gilson found the 7-piece dissection
that I mention on page 154.
After seeing my books, Bruce got in touch with me,
and I found out what he had been doing during the intervening four decades:
Bruce R. Gilson was born in 1942 in the Bronx, in New York City.
He earned B.S., M.S., and Ph.D. degrees in chemistry from
City College (1962), Yale University (1964),
and the University of Virginia (1969).
Since then, he has worked primarily in the computer programming field.
Bruce has maintained interests in
natural and constructed languages,
paper money from foreign countries,
public transportation,
unusual music scales,
and music from his boyhood years.
Bruce now lives in the Washington, DC area.
Gavin Theobald found a lovely 9-piece dissection of
a {12/2} to a square, using the completing the tessellation technique.
Although it has one more piece than another dissection
that Gavin found (on page 135),
this one turns no pieces over.
However, Gavin then went on to find an 8-piece dissection
with no pieces turned over!
Gavin illustrates
his new dissection on
his dodecagram webpage.
In March 2007,
Gavin Theobald found a lovely 12-piece dissection of
an {18} to a hexagon, using the completing the tessellation technique.
The dissection is based on Wolfgang Stöcher's technique
which he used to dissect any {3n} to an {n}.
(See Chapter 3 of Piano-Hinged Dissections: Time to Fold!)
Gavin's dissection involves a considerable reduction in the number of pieces from Stöcher's
for the particular case of n = 6, and furthermore turns no pieces over.
Copyright 1998-2007, Greg N. Frederickson.
Permission is granted to any purchaser of
Dissections: Plane & Fancy
to print out a copy
of this page for his or her own personal use.
Last updated April 13, 2020.