Recently, many individuals and groups have proposed neural algorithms for principal component analysis (PCA) and independent component analysis. In this project, I implemented three neural PCA and three neural ICA algorithms in Matlab and compared them. Additionally, I prepared a number of demonstration programs to illustrate the neural algorithms as well as PCA and ICA.
Principal component analysis has many applications, for example, classification and recognition problems [Diamantras]. PCA, and the closely related singular value decomposition, have applications from computer science to biomedical signal processing [Callaerts].
The goal of PCA is to find a set of orthogonal components that minimize the error in the reconstructed data. An equivalent formulation of PCA is to find an orthogonal set of vectors that maximize the variance of the projected data [Diamantras]. In other words, PCA seeks a transformation of the data into another frame of reference with as little error as possible, using fewer factors than the original data. For example, people often use PCA to reduce the dimensionality of data, that is, transforming m sensor readings into a set of n important factors in those readings.
In contrast to PCA, independent component analysis seeks, not a set of orthogonal components, but a set of independent components. The word independent is used in the statistical sense. Two components are independent if any knowledge about one implies nothing about the other. This condition is stronger than uncorrelated components.
ICA is also known as blind source separation. The blind source separation problem is to find the set of original sources from an observed mixture. One example is the “Cocktail” problem. In this problem the goal is to separate a series of individual sounds from observed mixtures. There are many demos of this problem (and ICA solutions) on the Web; the FastICA demo uses the non-neural FastICA algorithm.
I implemented, in Matlab, three neural PCA algorithms.
I also implemented three neural ICA algorithms.
Here, I present some of the results I found working with these networks.
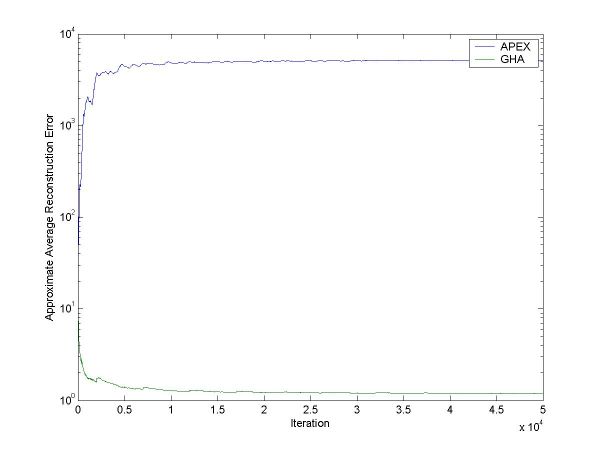
Using the error approximation from Giannakopoulos, I computed the error in the GHA and APEX algorithms while trying to learn a PCA subspace. Like Giannakopoulos, I distinguish between the well and poorly separated eigenvalue case. The following plots are generated by the pca_error_plots_separated.m and pca_error_plots_close.m files.

Figure 1: The approximate error in the PCA subspace for GHA and APEX when the eigenvalues are highly separated. GHA does much better than APEX in this case.
For figure 1, the exact errors after training are:
Final APEX error: 1078.203491
Final GHA error: 0.403387
Minimum error: 0.083081
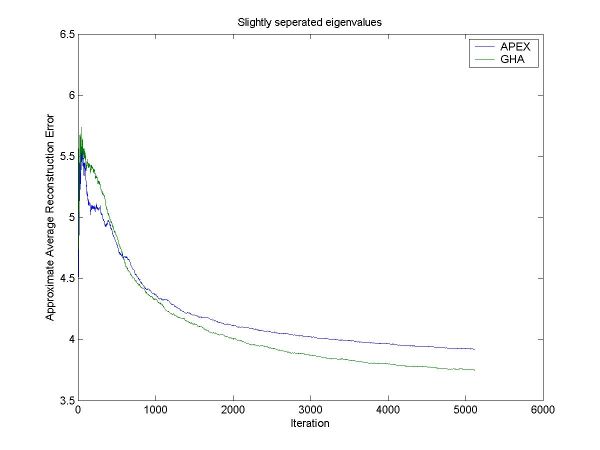
Figure 2: The approximate error in the PCA subspace for GHA and APEX when the eigenvalues are very similar. GHA only does slightly better than APEX in this case. Note that APEX converged faster initially.
For figure 2, the exact errors after training are:
Final APEX error: 3.822787
Final GHA error: 3.692088
Minimum error: 3.662126
Unfortunately, I do not have any error plots for ICA. I have, however, the following two examples to illustrate the unmixing ability of ICA.
The first example is a set of ECG recordings from a pregnant woman [Callaerts]. They show a clear heartbeat. The images are large, so I have included the figures as links.
Figure 3: The recordings of 8 ECG electrodes from a pregnant woman. The woman’s heartbeat is evident in these recordings.
Figure 4: The “unmixed” ECG recordings after one pass with the Bell and Sejnowski ICA algorithm, learning rate 0.001. The third signal is the baby’s heartbeat. The EASI algorithm never gave a good separation of the baby's heartbeat. The fetal_plots_bsica.m file implements this example.
Finally, I used ICA to “unmix” the following picture. The first row contains the source images, taken from CNN, resized and converted to luminosity images.

Figure 5: The top three images were mixed in a linear mixing channel into the bottom three images. While the first image appears "clean" the other two are masked by the mixing.

Figure 6: The first row ages is the result of Bell and Sejnowski's ICA algorithm on the mixed image data. The second row of images is the result of the EASI ICA algorithm on the mixed image data. The final row repeats the original, unmixed images again. EASI does not re-mix the "unmixed" soldier image, and extracts two fairly clean images from the mixture. Bell and Sejnowski's ICA algorithm does not do as well in this case; although Bell and Sejnowski's algorithm has separated other image mixtures using different random numbers -- try the ica_image_demo.m file to see this sample.
neural-pca-ica.zip
neural-pca-ica-methods-presentation.ppt
neural-pca-ica-results-presentation.ppt
Callaerts, Dirk. "Signal Separation Methods based on Singular Value Decomposition and their Application to the Real-Time Extraction of the Fetal Electrocardiogram from Cutaneous Recordings", Ph.D. Thesis, K.U.Leuven - E.E. Dept., Dec. 1989.
Cardoso, J. and B. Laheld. “Equivariant Adaptive Source Separation.” Transactions on Signal Processing, 44(12):3017-3030, 1996.
Comon, P. “Independent Component Analysis, a new concept?” In Signal Processing, 36:287-314, 1994.
Diamantras, K.I. and S. Y. Kung. Principal Component Neural Networks. John Wiley and Sons, 1996.
Fiori, S. “An Experimental Comparison of Three PCA Neural Networks.” Neural Processing Letters. 11(3):209-218, 2000.
Giannakopoulos, X., J. Karhunen, and E. Oja. “An Experimental Comparison of Neural ICA Algorithms.” Proc. Int. Conf. on Artificial Neural Networks, 651-656, 1998.
Karhunen, J. “Neural Approaches to Independent Component Analysis.” Proceedings of the 4th European Symposium on Artificial Neural Networks (ESANN '96), 1996.
Murata, N., K-R. Müller, A. Ziehe. “Adaptive On-line Learning in Changing Environments.” Advances in Neural Information Processing Systems, 9:599, 1997.
Oursland, A., J. D. Paula, and N. Mahmood. “Case Studies in Independent Component Analysis.”