The future of the Lake Arrowhead matrix
Cleve Moler just wrote a fantastic blog post about the Lake Arrowhead graph. The Lake Arrowhead graph, or the Golub Graph as I like call it, was a coauthor graph centered around Gene collected at the 1993 Householder meeting in Lake Arrowhead, California. We'll study this network using a few one-liner Matlab link-prediction techniques. These are all matrix equations that Gene would have enjoyed, so this is a fitting tribute. We'll see which predicts the most correct links in the top 25 (with at most 5 predictions for any author ...)
There are few issues with the Matlab code that would ruffle the feathers of any numerical analysis. Namely, I've used the inv function to greatly simplify the codes. Hopefully we can agree it's okay for this simple example.
I've decided to crowdsource the actual ranking! Please vote for which list you think looks "most right"!
Contents
- Download the network
- Load the network and look at it.
- Remove self-loops
- Katz scores
- Katz scores with a tight and nearly diagonally dominant, matrix
- Katz scores with a matrix that's very DD
- PageRank with alpha = 0.85
- PageRank with alpha = 0.5
- PageRank with alpha = 0.99
- The matrix exponential
- The matrix exponential with the normalized Laplacian
- Commute time
- Appendix
Download the network
Visit Gilbert's original website and download the tar.Z file, unzip it, proceed into the householder directory, and turn the "drawit.m" file into a function.
Load the network and look at it.
The drawit function is included in the tar file with the graph. We do need to edit it, so convert it into a function, otherwise you won't get nice figures below
load housegraph; n = size(A,1); drawit axis off;
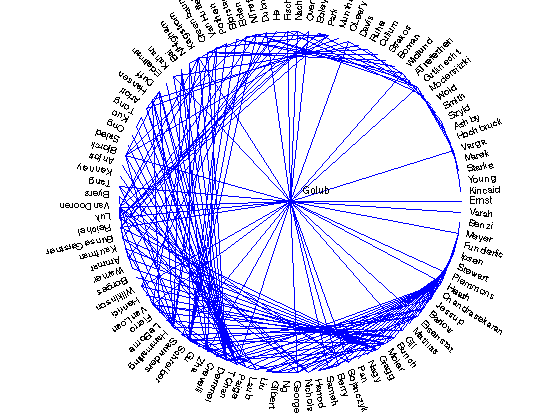
Remove self-loops
When we are predicting the future, allowing self-loops hardly seems fair! Although, in truth, they have a fairly predictable affect on each of the methods we study. It's just easier to remove them.
B = A - diag(diag(A));
Katz scores
Leo Katz wrote a fantastic paper in 1953 on a new way to determine a "status index" that measures how important someone is in a social network. More recently, the Katz score between a pair of nodes was shown to predict links that would form in the future. See this paper by Jon Kleinberg (http://www.cs.cornell.edu/home/kleinber/link-pred.pdf) and some recent work by Inderjit Dhillon (http://www.cs.utexas.edu/users/inderjit/Talks/2010-IPAM-Inderjit.pdf)
The Katz score between node i and j is the number of walks between the nodes, where the weight of a walk of length k is alpha^k. These scores are usually defined via the Neumann series:
K = alpha*A + alpha^2*A^2 + alpha^3*A^3 + ...
which expresses the score for all pairs of nodes simultaneously. The relationship with the Neumann series means that we can evaluate this infinite series in Matlab using a single matrix inverse:
K = inv(eye(n) - alpha*A)
Picking alpha is always the key question with this method. While the inverse exists as long as alpha isn't one of a very few special values related to the eigenvalues of A, most of these choices are rotten. Choosing alpha = 1/largest degree is common as it'll make the Neumann series converge. We evaluate this value as well as a smaller value of alpha that should favor short connections instead of longer connections.
That's a long-winded explaination for the next three lines of Matlab code to actually compute them!
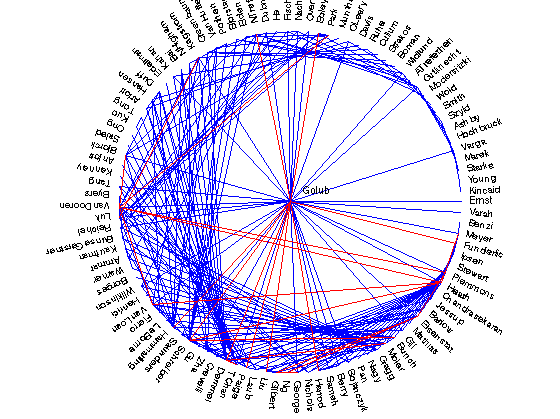
Katz scores with a tight and nearly diagonally dominant, matrix
fprintf('\nKatz scores with DD matrix\n');
alpha = 1./max(sum(B,2));
showpreds(inv(eye(n) - alpha*B),A,25,name);
Katz scores with DD matrix
Golub - Paige with value 0.005967
Golub - Demmel with value 0.005407
Golub - Schreiber with value 0.005146
Golub - Hammarling with value 0.004965
Schreiber - Heath with value 0.004887
VanLoan - VanDooren with value 0.004752
TChan - Demmel with value 0.004682
VanLoan - Heath with value 0.003874
Eisenstat - Plemmons with value 0.003845
Golub - Liu with value 0.003818
VanDooren - Heath with value 0.003796
VanDooren - Plemmons with value 0.003785
Golub - Funderlic with value 0.003717
Golub - Harrod with value 0.003699
Golub - Boley with value 0.003698
Moler - Demmel with value 0.003689
Golub - NTrefethen with value 0.003660
George - Gilbert with value 0.003645
Heath - Meyer with value 0.003609
Eisenstat - Ng with value 0.003602
Bjorck - VanDooren with value 0.003589
Kagstrom - Luk with value 0.003563
Gilbert - Eisenstat with value 0.003547
Park - VanDooren with value 0.003488
Schreiber - Bunch with value 0.003483
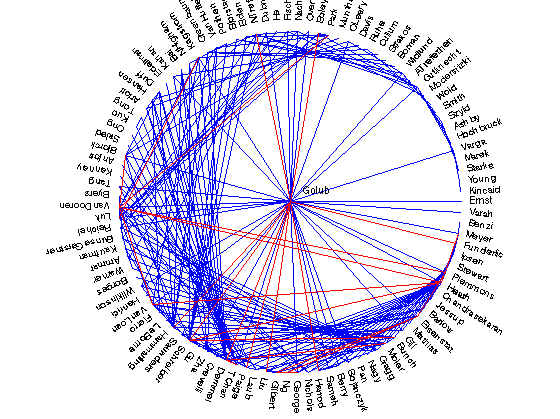
Katz scores with a matrix that's very DD
fprintf('\nKatz scores with very DD matrix\n'); alpha = 1./max(sum(B,2)+100); % smaller alpha bound showpreds(inv(eye(n) - alpha*B),A,25,name);
Katz scores with very DD matrix
Golub - Paige with value 0.000298
Golub - Demmel with value 0.000245
Golub - Schreiber with value 0.000242
Golub - Hammarling with value 0.000240
Schreiber - Heath with value 0.000240
VanLoan - VanDooren with value 0.000239
TChan - Demmel with value 0.000238
VanLoan - Heath with value 0.000182
Eisenstat - Plemmons with value 0.000182
Golub - Liu with value 0.000181
VanDooren - Heath with value 0.000181
VanDooren - Plemmons with value 0.000181
Moler - Demmel with value 0.000181
George - Gilbert with value 0.000180
Golub - Funderlic with value 0.000180
Golub - Harrod with value 0.000180
Golub - Boley with value 0.000180
Eisenstat - Ng with value 0.000180
Golub - NTrefethen with value 0.000180
Heath - Meyer with value 0.000179
Bjorck - VanDooren with value 0.000179
Kagstrom - Luk with value 0.000179
Gilbert - Eisenstat with value 0.000179
Park - VanDooren with value 0.000179
Schreiber - Bunch with value 0.000178
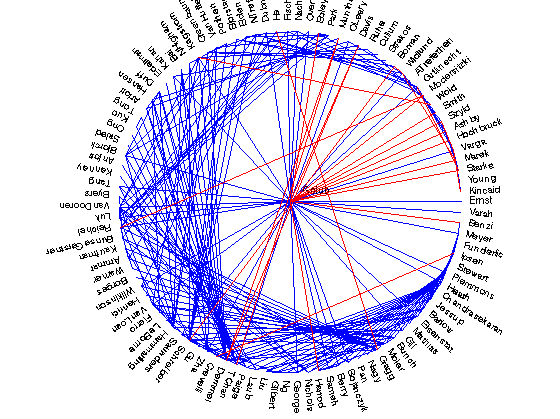
PageRank with alpha = 0.85
PageRank is typically used for finding the most important links on a web-page. However, it can just as easy be used to determine which links are most likely to form in the future! We compute the PageRank value for each node, where it "teleports" back to itself as a link-prediction measure.
Alpha = 0.85 is the standard value of alpha in PageRank. Let's see what predictions we get with this method. The output is a non-symmetric matrix and so we'll symmetrize it by taking the best prediction for each user.
fprintf('\nPageRank with alpha = 0.85\n');
alpha = 0.85;
symmax = @(X) max(X,X');
showpreds(symmax(inv(eye(n) - alpha*B*diag(1./sum(B,2)))),A,25,name)
PageRank with alpha = 0.85
Crevelli - Ipsen with value 0.874633
Kincaid - Varga with value 0.866249
Wold - Kagstrom with value 0.699082
Golub - Modersitzki with value 0.661777
Golub - Davis with value 0.579365
Gutknecht - Starke with value 0.564489
Widlund - Boman with value 0.526378
He - Gragg with value 0.520894
Golub - Smith with value 0.512122
Varga - Hochbruck with value 0.508966
Schreiber - Boman with value 0.490197
Davis - Demmel with value 0.483887
TChan - MuntheKaas with value 0.478409
MuntheKaas - Demmel with value 0.451077
Golub - Ashby with value 0.447502
Modersitzki - Reichel with value 0.446283
Golub - Szyld with value 0.434651
Golub - Harrod with value 0.431189
Golub - Marek with value 0.420211
Marek - Widlund with value 0.412368
Golub - Benzi with value 0.406861
Golub - Boley with value 0.405866
Golub - Starke with value 0.403452
Varga - Szyld with value 0.401111
Golub - Hochbruck with value 0.395218
PageRank with alpha = 0.5
fprintf('\nPageRank with alpha = 0.5\n');
alpha = 0.5;
symmax = @(X) max(X,X');
showpreds(symmax(inv(eye(n) - alpha*B*diag(1./sum(B,2)))),A,25,name)
PageRank with alpha = 0.5
Crevelli - Ipsen with value 0.159729
Kincaid - Varga with value 0.157497
Wold - Kagstrom with value 0.149887
Golub - Modersitzki with value 0.110927
Gutknecht - Starke with value 0.108330
Widlund - Boman with value 0.103562
Golub - Davis with value 0.101269
Schreiber - Boman with value 0.099594
Modersitzki - Reichel with value 0.098967
Davis - Demmel with value 0.098850
Varga - Hochbruck with value 0.098413
He - Gragg with value 0.094472
TChan - MuntheKaas with value 0.084800
MuntheKaas - Demmel with value 0.082447
Marek - Widlund with value 0.078260
MuntheKaas - Duff with value 0.076992
Varga - Szyld with value 0.076467
Golub - Smith with value 0.072827
Pothen - Demmel with value 0.066630
Cullum - Demmel with value 0.065399
Strakos - Demmel with value 0.065399
Kenney - Paige with value 0.063973
Chandrasekaran - Jessup with value 0.063891
Cullum - Hammarling with value 0.062903
Strakos - Hammarling with value 0.062903
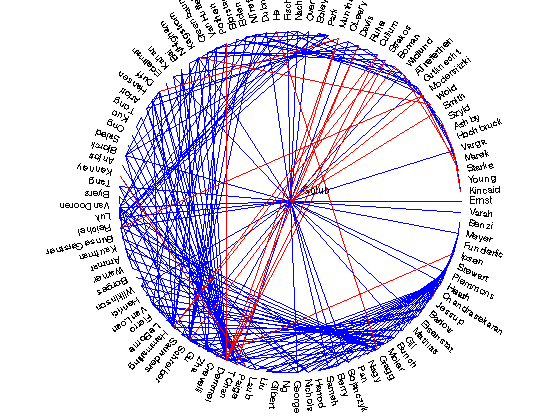
PageRank with alpha = 0.99
For a while, people were convinced that solving PageRank with alpha ~ 1 was the right thing to do as it kept the results as close to the graph as possible. For web-graphs, this is wrong as Vigna and his collaborators showed. However, for graphs that are strongly connected, it's still interesting. Let's see what we get!
fprintf('\nPageRank with alpha = 0.99\n');
alpha = 0.99;
symmax = @(X) max(X,X');
showpreds(symmax(inv(eye(n) - alpha*B*diag(1./sum(B,2)))),A,25,name)
PageRank with alpha = 0.99
Golub - Modersitzki with value 7.740538
Golub - Davis with value 7.551120
Golub - Smith with value 7.516129
Golub - Szyld with value 7.425185
Golub - Ashby with value 7.411030
Golub - Marek with value 7.408324
Golub - Starke with value 7.373870
Golub - Hochbruck with value 7.355581
Golub - Harrod with value 7.329255
Golub - Young with value 7.320046
Golub - Boley with value 7.316955
Golub - Nagy with value 7.284151
Golub - Pan with value 7.284151
Golub - Benzi with value 7.269946
Golub - Hansen with value 7.248056
Golub - Kincaid with value 7.246845
Golub - Funderlic with value 7.240728
Golub - Gu with value 7.235458
Golub - Paige with value 7.230160
Golub - Park with value 7.222309
Golub - NTrefethen with value 7.219603
Golub - Bjorstad with value 7.202310
Golub - VanHuffel with value 7.189794
Golub - Ruhe with value 7.182335
Golub - Liu with value 7.161991
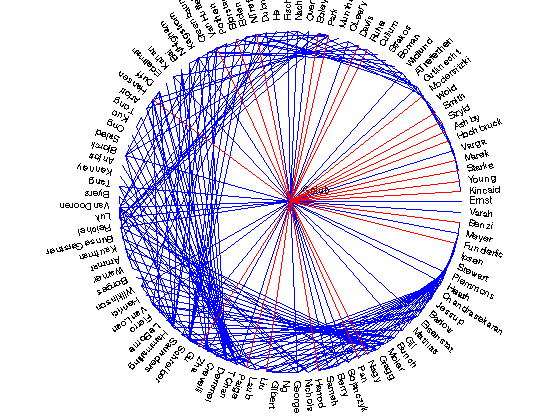
The matrix exponential
Benzi, Higham, and Estrada have written about using the matrix exponential for analyzing social networks. Let's see what we get here.
fprintf('\nMatrix exponential with adjacency\n');
showpreds(expm(B),A,25,name);
Matrix exponential with adjacency
Golub - Demmel with value 200.667542
Golub - Schreiber with value 163.492101
Golub - Hammarling with value 134.885201
Golub - Paige with value 133.287838
Golub - Liu with value 107.695220
VanLoan - Heath with value 105.109816
VanDooren - Heath with value 104.281025
Golub - Moler with value 103.008898
VanDooren - Plemmons with value 96.089354
Golub - Laub with value 93.927783
Schreiber - Heath with value 93.858705
Golub - Gilbert with value 93.130294
Plemmons - Demmel with value 91.019041
VanLoan - Plemmons with value 89.104026
Golub - Barlow with value 88.970881
Golub - Ng with value 87.220015
Golub - Duff with value 87.169014
Eisenstat - Plemmons with value 87.001184
Golub - Funderlic with value 86.966110
Luk - Heath with value 85.078033
VanDooren - Demmel with value 81.426481
VanLoan - VanDooren with value 80.838813
Luk - Plemmons with value 79.727039
Golub - Harrod with value 78.072424
Kagstrom - Heath with value 77.667173
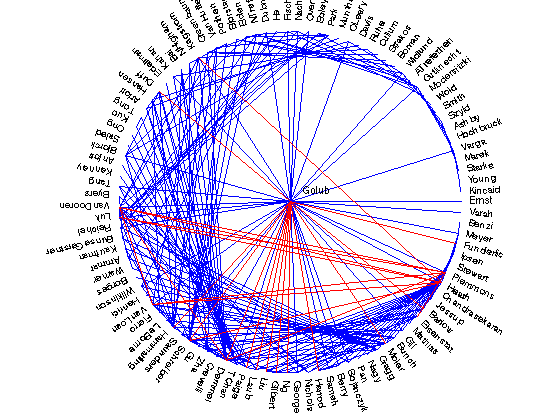
The matrix exponential with the normalized Laplacian
Based on work with PageRank, and Fan Chung Graham's "Heat-Kernel PageRank" version, I've often wondered how well the matrix exponential with the normalized Laplacian does instead ...
fprintf('\nMatrix exponential with normalized Laplcian\n');
Dhalf = diag(sqrt(1./sum(B,2)));
L = eye(n) - Dhalf*A*Dhalf;
showpreds(expm(L),A,25,name);
Matrix exponential with normalized Laplcian
Varga - Hochbruck with value 0.201888
Gutknecht - Starke with value 0.190164
Crevelli - Ipsen with value 0.187998
Kincaid - Varga with value 0.187151
Wold - Kagstrom with value 0.184371
BunseGerstner - Ammar with value 0.178577
Marek - Widlund with value 0.153282
Varga - Szyld with value 0.152184
He - Gragg with value 0.142192
Cullum - Strakos with value 0.138646
Widlund - Boman with value 0.131688
Chandrasekaran - Jessup with value 0.118900
Modersitzki - Reichel with value 0.117852
Smith - Szyld with value 0.117272
He - Byers with value 0.110082
Bunch - Hansen with value 0.107937
Bjorstad - Smith with value 0.102005
Fierro - OLeary with value 0.100629
Young - Starke with value 0.099905
Marek - Young with value 0.099319
OLeary - Smith with value 0.098833
Park - VanDooren with value 0.098414
Marek - Starke with value 0.098340
LeBorne - Fierro with value 0.097025
Bai - VanHuffel with value 0.093191
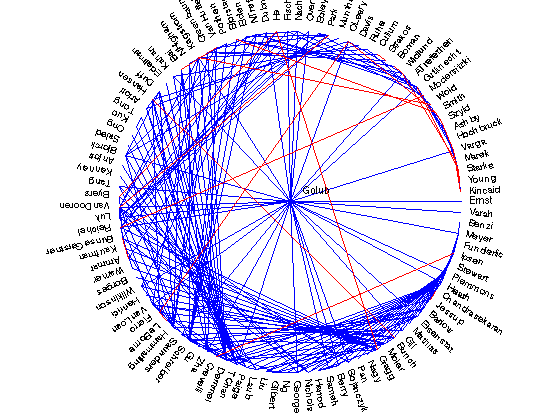
Commute time
The commute time distance between two nodes of a graph is the expected time for a random walk started at one node to first the second node, and then return back to the first node. Pairs of nodes with no edges and small commute time distance are ones that are likely to form edges in the future. Let's see how this measure does!
fprintf('\nCommute time\n'); K = diag(sum(B,2)) - B; C = zeros(n,n); Ki = pinv(full(K)); for i=1:n, for j=1:n, C(i,j) = Ki(i,i) + Ki(j,j) - 2*Ki(i,j); end, end showpreds(-C,A,25,name); % small commute times are likely "new links"
Commute time
Golub - Demmel with value -0.143612
Golub - Schreiber with value -0.165561
Golub - Hammarling with value -0.181163
Schreiber - Heath with value -0.217498
VanDooren - Demmel with value -0.223000
Golub - Moler with value -0.230225
Plemmons - Demmel with value -0.232642
VanDooren - Heath with value -0.241182
Golub - Paige with value -0.245504
VanDooren - Plemmons with value -0.252665
VanLoan - Heath with value -0.256789
Schreiber - Hammarling with value -0.257972
VanLoan - VanDooren with value -0.258443
Schreiber - VanDooren with value -0.259069
Hammarling - Heath with value -0.259965
Golub - Gragg with value -0.260218
Schreiber - Plemmons with value -0.262964
Moler - Demmel with value -0.265665
TChan - Demmel with value -0.276060
Moler - Heath with value -0.277328
VanLoan - Hammarling with value -0.280051
Hammarling - Plemmons with value -0.280855
VanLoan - Plemmons with value -0.288621
George - Schreiber with value -0.291199
Luk - Demmel with value -0.293697
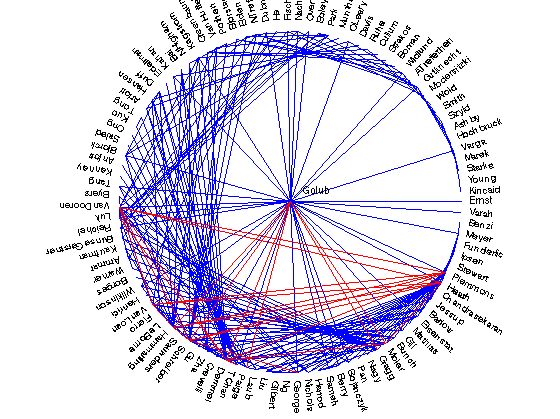
Appendix
You need two extra routines for this code:
type drawit
function drawit
% DRAWIT Script to plot the graph of coauthors from Householder 93.
load housegraph;
% A is the adjacency matrix.
% prcm is a permutation; any permutation could be substituted.
% name is the vector of people's names.
% xy is just xy coords of points on the unit circle (and the origin).
Aperm = A(prcm,prcm);
nameperm = name(prcm,:);
nfolks = max(size(A));
clf
gplot(Aperm,xy);
axis off;
axis square;
x = xy(:,1) * 1.05;
y = xy(:,2) * 1.05;
x(1) = .08; % Put names(1) in the center of the circle.
y(1) = .06;
h = text(x,y,nameperm);
for k = 2:nfolks % Shrink the font for the other names, and rotate them.
set(h(k),'fontsize',10);
set(h(k),'rotation',180/pi*atan2(y(k),x(k)));
end;
type showpreds
function showpreds(P,G,k,names)
n = size(P,1);
P = P - spones(G).*P; % remove all the given links
[i,j,v] = find(triu(P,1)); % remove any self-loops
[~,p] = sort(v,'descend');
cnt = zeros(n,1);
cur=0;
Preds = zeros(k,2);
for pi=p(:)'
if cur >= k, break; end
li=i(pi); lj=j(pi);
if cnt(li) > 5 && cnt(lj) > 5, continue; end
fprintf(' %20s - %-20s with value %f \n', ...
deblank(names(li,:)), names(lj,:), v(pi));
cnt(li) = cnt(li)+1; cnt(lj)=cnt(lj)+1;
cur = cur+1;
Preds(cur,1) = li; Preds(cur,2) = lj;
end
% Display them
Preds = sparse(Preds(:,1),Preds(:,2),1,n,n);
load housegraph;
drawit;
hold on; gplot(Preds(prcm,prcm),xy,'r.-'); hold off;
axis square;