Monte Carlo Simulation of the PageRank Random Surfer

Google created the PageRank random surfer to model how someone might browse the web without any particular goal in mind. Their idea was to determine, based solely on the links of the web, which are the most important pages. In particular, they wanted to use this to differentiate between the real "Sports Illustrated" and many other pages out there that just contain the term "Sports Illustrated." And they wanted to do this all types of businesses, not just those that are obvious like Sports Illustrated.

Here's a story from Lance Fortnow about the impact this had compared with the best search engine of the day:

http://blog.computationalcomplexity.org/2013/07/altavista-versus-google.html

But I digress, the PageRank random surfer is an entity that:

  • with probability α, follows a random link from the current page
  • with probability (1-α), jumps to a random node in the graph.

The PageRank score of a page is the probability of finding the surfer on that page after a large number of steps.

Step 1: Setup the adjacency matrix

In the following code, we establish the adjacency matrix from class.

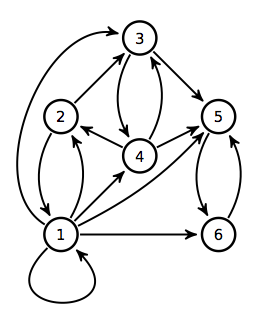
A graph

In [2]:
A = [1 1 1 1 1 1;
     1 0 1 0 0 0;
     0 0 0 1 1 0;
     0 1 1 0 1 0;
     0 0 0 0 0 1;
     0 0 0 0 1 0]
alpha = 1/2
; # don't output anything in IJulia

Let's see how we can access information from the adjacency matrix.

In [5]:
find(A[5,:])
Out[5]:
1-element Array{Int64,1}:
 6
In [23]:
"""
`random_walk_step`
==================
This function uses the global variable A to
take a step of a random walk in the graph
represented by A.

`next = random_walk_step(page)` takes one
step of the PageRank random walk and
returns the subsequent page.

At each step, the surfer tosses a biased
coin. With probability alpha, the surfer
follows a link in the page. Otherwise the
surfer jumps to a random page.
"""
function random_walk_step(page)
    follow_link = rand() <= alpha
    if follow_link
        next = rand(find(A[page,:]))
        #println("Followed link from "*string(page)*" to "*string(next))
    else
        next = rand(1:size(A,1))
        #println("  Jumped from "*string(page)*" to "*string(next))
    end
    return next
end
@show random_walk_step(1)

random_walk_step(1) = 3
Out[23]:
3

Step 3: Do the Monte Carlo estimate.

Here, we run a Monte Carlo estimate of the random walk, starting from page 1.

In [28]:
n = size(A,1)
visits = zeros(Int64,n)
nsteps = 10000000
page = 1
for i=1:nsteps
    page = random_walk_step(page)
    visits[page] += 1
end
visits/nsteps
Out[28]:
6-element Array{Float64,1}:
 0.122236
 0.115053
 0.144044
 0.129472
 0.26375 
 0.225445

Step 4: Does the starting page matter?

Wait, you say, you started on Page 1! That's not far, we should have started on a random page. Let's see if this changes anything.

In [ ]:
# n = size(A,1)
visits = zeros(Int64,n)
nsteps = 1000000
page = rand(1:size(A,1))
for i=1:nsteps
    page = random_walk_step(page)
    visits[page] += 1
end
visits/nsteps

Not really. This is because after a jump step, the starting page doesn't matter at all.